Keskiarvon poikkeama: kaikki, mitä tarvitset tietää kyselyistä.

Kuvittele, että teet asiakastyytyväisyyskyselyn suositulle kahvilaketjulle. Odotat useimpien asiakkaiden arvioivan kahvin korkealle, sillä kahvilasi ylpeilee laadunvalvonnalla ja erinomaisella palvelulla. Kun kuitenkin tarkastelet tuloksia, arviot ovat hajanaisia. Jotkut asiakkaat antavat kiittäviä arvioita, kun taas toiset näyttävät kokeneen huonon palvelun. Mitä on tapahtunut? Tässä kohtaa vaihtelu (standard deviation) auttaa kvantifioimaan tietosi, mikä mahdollistaa sen ymmärtämisen, ovatko saadut vastaukset lähellä toisiaan vai vaihtelevatko ne suuresti. Tämän menetelmän avulla voit selvittää, ovatko ne muutamat matalat pisteet poikkeavia vai onko brändisi tarjoukset todella epäjohdonmukaisia. Mitkä ovat vaihtelun (standard deviation) perusteet? Perustaltaan vaihtelu mittaa, kuinka laajasti arvot datassa jakautuvat. Se kertoo, kuinka paljon yksittäiset vastaukset poikkeavat keskiarvosta, mikä auttaa ymmärtämään, onko tietosi johdonmukaisia vai sisältävätkö ne merkittävää vaihtelua. Kyselyanalyysissä vaihtelu antaa syvällisempiä näkemyksiä siihen, miten ihmiset vastaavat, ja tekee siitä arvokkaan työkalun tulosten tulkintaan. Esimerkiksi, jos kaikki asiakkaasi arvioivat palvelusi 8 tai 9, sinulla on pieni vaihtelu, mikä tarkoittaa, että tulokset ovat melko johdonmukaisia. Toisaalta, jos jotkut arvioivat sen 2 ja toiset 10, vaihtelu on paljon suurempaa, mikä viittaa monipuolisempiin mielipiteisiin. Vaihtelun symboli on “σ” (pieni sigma) väestön vaihtelulle ja “sss” otoksen vaihtelulle. Se on lyhenne, jota käytetään tilastollisissa kaavoissa ja kaavastoissa merkkaamaan vaihtelua. Vaihtelun merkitys kyselyissä Vaihtelu antaa mittarin vastausten luotettavuudelle. Vaikka keskiarvo (mean) voi antaa sinulle nopean yhteenvedon, vaihtelu lisää kontekstia. Se näyttää, ovatko useimmat vastaukset keskiarvon ympärillä vai jakautuvatko ne laajalle. Pieni vaihtelu viittaa johdonmukaisuuteen, kun taas suuri vaihtelu osoittaa vaihtelevuutta, mikä voi viitata tulkinta- tai kokemuseroihin. Tämä mittaus antaa tutkimuslaitoksille ja yrityksille mahdollisuuden nähdä kyselyaineiston pinnan yli, auttaa tunnistamaan alueita, joilla mielipiteet poikkeavat, ja lopulta ohjaamaan tarkennettuja parannuksia tai muutoksia. Vaihtelun laskeminen askel askeleelta esimerkin kanssa Vaihtelun laskeminen saattaa aluksi vaikuttaa monimutkaiselta, mutta se on vaiheittainen prosessi, joka helpottuu harjoituksen myötä. Aloita laskemalla datasi keskiarvo. Sitten vähennä keskiarvo jokaisesta datapisteestä, neliöi tulos ja laske näiden neliöityjen erojen keskiarvo. Lopuksi ota tämän keskiarvon neliöjuuri saadaksesi vaihtelun. 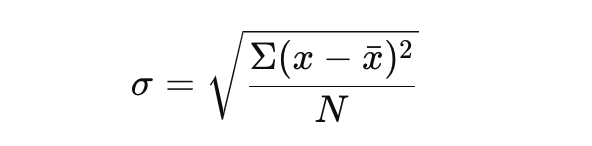Aloitetaan käyttämällä seuraavaa kaavaa: Tämä kaava antaa sinulle selkeän käsityksen datasi vaihtelusta. Kuvitellaan, että teit kyselyn, jossa pyysit 5 asiakasta arvioimaan tyytyväisyytensä palveluusi asteikolla 1-10. Vastaukset olivat: 7, 8, 6, 9, 10. Katsotaan nyt vaihtelua tämän datan avulla: Askel 1: Laske keskiarvo Laske keskiarvo lisäämällä kaikki datapisteet yhteen ja jakamalla vastausten määrällä. 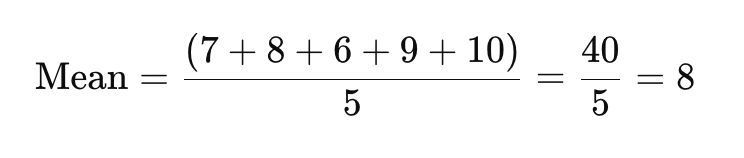Keskiarvo tässä on 8. 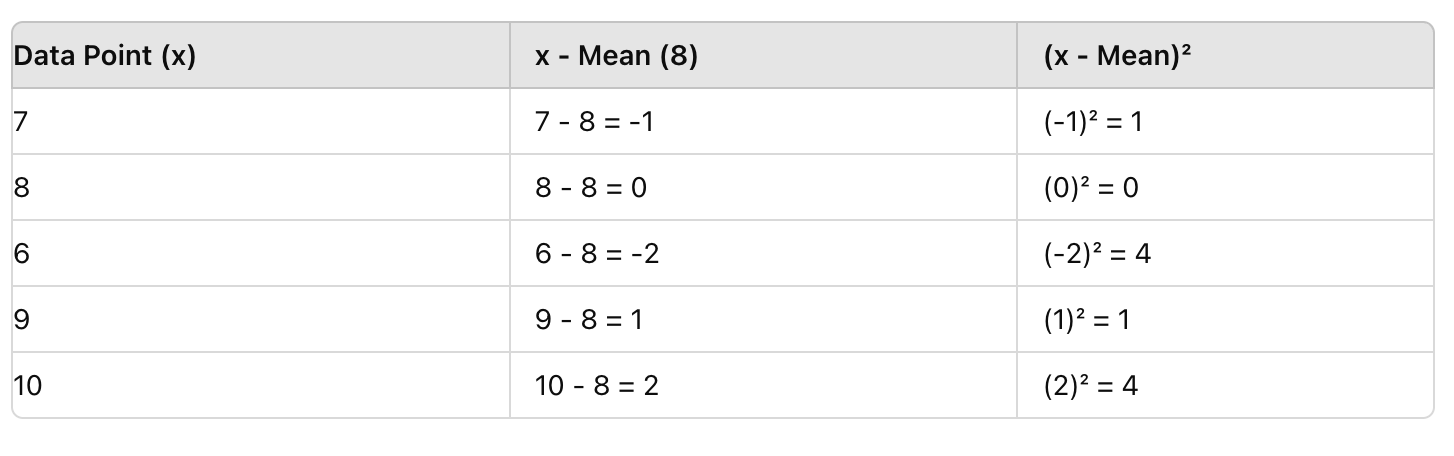Askel 2: Vähennä keskiarvo jokaisesta datapisteestä ja neliöi tulos Seuraavaksi vähennä jokaisesta arvosta keskiarvo (8), ja neliöi tulos. Tämä poistaa negatiiviset arvot ja korostaa poikkeamia. Askel 3: Laske neliöityjen erojen keskiarvo Lisää nyt neliöidyt erot yhteen ja jaa datapisteiden määräksesi saadaksesi varianssin. 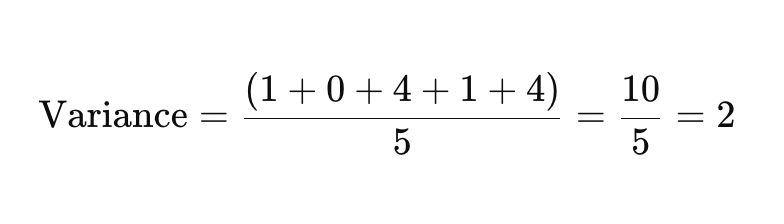Askel 4: Ota varianssin neliöjuuri Lopuksi ota varianssin neliöjuuri saadaksesi vaihtelun. Tässä esimerkissä vaihtelu on noin 1.41. Tämä tarkoittaa, että useimmat asiakastyytyväisyysarviot ovat 1.41 pistettä keskiarvon (8) sisällä. Koska vaihtelu on suhteellisen pieni, arviot ovat melko lähellä keskiarvoa, mikä osoittaa palautteen johdonmukaisuuden. Jos vaihtelu olisi suurempi, esimerkiksi 3 tai 4, se viittaisi laajempaan vastauksen jakaantumiseen, johon jotkut asiakkaat olisivat tyytyväisempiä tai tyytymättömämpiä kuin toiset. Vaihtelu Excelissä Vaiheittainen opas vaihtelun laskemiseen Excelissä Microsoft Excel tai Google Sheets on yksi kätevimmistä työkaluista vaihtelun laskemiseen. Tässä on, miten se tehdään: Syötä data sarakkeeseen. Valitse tyhjää solua, johon haluat tuloksen. Käytä kaavaa =STDEV.P() väestön vaihtelulle tai =STDEV.S() otoksen vaihtelulle. Valitse datasi, paina Enter, ja Excel laskee tuloksen heti. Excel automatisoi prosessin, säästäen aikaa ja vähentäen manuaalisten virheiden mahdollisuutta. Exportointi LimeSurveysta Exceliin LimeSurveylla voit viedä kyselydatasi suoraan Exceliin tulosten syvempää analysointia varten. Tee se seuraavasti: Siirry tulososioon LimeSurveyssa. Valitse vientivaihtoehto ja valitse Excel muotona. Kun olet vienyt, käytä Excelin tilastollisia toimintoja, mukaan lukien vaihtelun, syvempien tietojesi ymmärtämiseksi. Yhdistämällä LimeSurvey'n tietojen keräyskyvyt Excelin analyysityökaluihin voit tehokkaasti tulkita ja toimia kyselytulosten perusteella. Vaihtelun ymmärtäminen Vaihtelu vs. standardivirhe Vaihtelu ja standardivirhe liittyvät toisiinsa, mutta palvelevat eri tarkoituksia. Vaihtelu mittaa yksittäisten datapisteiden jakautumista, kun taas standardivirhe mittaa otoskeskihinnan tarkkuutta verrattuna todelliseen väestön keskiarvoon. Kyselyissä vaihtelu auttaa sinua ymmärtämään vastausten vaihtelua, kun taas standardivirhe on hyödyllinen arvioitaessa, kuinka lähellä otoskeskihinta on todellista väestön keskiarvoa. Vaihtelu vs. varianssi Varianssi on toinen mittari datan hajaantumiselle, ja se on vaihtelun neliö. Vaikka varianssi auttaa kvantifioimaan vaihtelun suuruutta, vaihtelu on helpompi tulkita, koska se on ilmaistu samoissa yksiköissä kuin alkuperäinen datasi. Esimerkiksi, jos mittaat tyytyväisyysarvioita, vaihtelu antaa intuitiivisen käsityksen siitä, kuinka paljon vastaukset eroavat keskiarvosta. Vaihtelun tulosten tulkitseminen Kun olet laskenut vaihtelun, voit käyttää sitä arvioidaksesi kyselyvastauksesi johdonmukaisuutta. Matala vaihtelu tarkoittaa, että vastaajat ovat yleensä samaa mieltä, kun taas korkea vaihtelu viittaa vaihtelevaan mielipiteeseen. Kuvitellaan, että kyselit 100 työntekijältä heidän työtyytyväisyyttään asteikolla 1-10. Jos useimmat vastaukset ovat keskittyneet 8 ympärille pienen vaihtelun kanssa, se viittaa yleiseen tyytyväisyyteen. Kuitenkin, jos arviot vaihtelevat 4-10, suurempi vaihtelu osoittaa, että mielipiteet ovat jakautuneita, ja saatat tarvita syvempää tutkimusta. Vaihtelun käytännön sovellukset Kysymysten parantaminen: Jos huomaat suuren vaihtelun tiettyyn kysymykseen, se voi viitata siihen, että kysymys on epäselvä tai ei ymmärretty hyvin vastaajien toimesta. Sanamuodon tarkentaminen voi auttaa keräämään tarkempaa dataa tulevissa kyselyissä. Tietoperusteisten päätösten tekeminen: Vaihtelu auttaa sinua tekemään tietoisempia päätöksiä paljastamalla kaavoja kyselydatassasi. Esimerkiksi, jos palaute on erittäin vaihtelevaa, voit jakaa yleisösi ja muokata vastaustasi sen mukaisesti. Tarkkuuden varmistaminen vaihtelussa Puuttuvat tiedot: Puuttuvat tiedot voivat vääristää vaihtelun laskentaa. Vääristymien välttämiseksi ota joko puuttuvat tiedot huomioon jättämällä pois puutteelliset vastaukset tai käytä imputointitekniikoita. Poikkeamien välttäminen: Datan tarkistaminen virheiden tai poikkeamien varalta on oleellista. Jopa yksi virheellinen syöttö voi merkittävästi muuttaa tuloksiasi. LimeSurvey'n kyselytyökalujen käyttö voi auttaa sinua keräämään tarkkaa ja käyttökelpoista dataa, joka heijastaa todellista vaihtelua. Käyttämällä vaihtelun ymmärrystä avaat voimakkaita näkemyksiä kyselytuloksistasi. Tämä ei vain mahdollista datan tehokkaampaa tulkitsemista, vaan myös parempien päätösten tekemistä perustuen syvempään ymmärrykseen siitä, mitä vastaajasi ajattelevat, kokevat tai toimivat. Kun olet määrittänyt vaihtelun, LimeSurvey antaa sinun parantaa kysymyksiäsi, jotta voit hyödyntää kyselyäsi ja tietojasi parhaalla mahdollisella tavalla. Kokeile sitä tänään!