ค่าเบี่ยงเบนมาตรฐาน: ทุกสิ่งที่คุณต้องรู้เกี่ยวกับการสำรวจ

ลองจินตนาการว่าคุณทำการสำรวจความพึงพอใจของลูกค้าในร้านกาแฟชื่อดัง คุณคาดหวังว่าลูกค้าส่วนใหญ่จะให้คะแนนกาแฟสูง เพราะร้านของคุณมีชื่อเสียงด้านการควบคุมคุณภาพและบริการที่ยอดเยี่ยม แต่เมื่อลองดูผลลัพธ์แล้ว คะแนนจะอยู่กระจายสุดๆ บางคนให้คะแนนดีเลิศ ขณะที่บางคนดูเหมือนจะมีประสบการณ์ไม่ดี แล้วนี่เกิดอะไรขึ้น? นี่คือจุดที่ค่าเบี่ยงเบนมาตรฐานช่วยในการวัดข้อมูล ทำให้คุณเข้าใจว่าความคิดเห็นที่ได้รับมีความใกล้เคียงกันหรือแตกต่างกันอย่างมาก ด้วยวิธีนี้ คุณสามารถค้นหาว่าคะแนนต่ำเหล่านั้นเป็นค่าผิดปกติหรือผลิตภัณฑ์ของแบรนด์คุณมีความไม่สอดคล้องกันจริงๆ ค่าเบี่ยงเบนมาตรฐานคืออะไร? โดยพื้นฐานแล้ว ค่าเบี่ยงเบนมาตรฐานใช้วัดว่าค่าต่างๆ ในชุดข้อมูลมีการกระจายตัวมากน้อยเพียงใด มันบอกคุณว่าคำตอบแต่ละอันมีความเบี่ยงเบนจากค่าเฉลี่ยเท่าไหร่ ช่วยให้คุณเข้าใจว่าข้อมูลของคุณมีความสอดคล้องหรือมีความแปรปรวนที่สำคัญ ในการวิเคราะห์สำรวจ ค่าเบี่ยงเบนมาตรฐานจะให้ข้อมูลเชิงลึกเกี่ยวกับวิธีที่ผู้คนตอบสนอง ทำให้เป็นเครื่องมือที่มีค่าที่ใช้ในการตีความผลลัพธ์ ตัวอย่างเช่น หากลูกค้าทั้งหมดให้คะแนนบริการของคุณ 8 หรือ 9 จาก 10 คุณจะมีค่าเบี่ยงเบนมาตรฐานที่เล็กน้อย แทนที่ผลลัพธ์จะค่อนข้างสอดคล้องกัน ในทางตรงกันข้าม หากบางคนให้คะแนนเป็น 2 และบางคนเป็น 10 ค่าเบี่ยงเบนมาตรฐานจะใหญ่ขึ้นมาก บ่งบอกถึงความคิดเห็นที่หลากหลาย สัญลักษณ์สำหรับค่าเบี่ยงเบนมาตรฐานคือ “σ” (ซิกมาลowercase) สำหรับเบี่ยงเบนมาตรฐานของประชากร และ “sss” สำหรับเบี่ยงเบนมาตรฐานของตัวอย่าง เป็นการย่อที่ใช้ในสมการและสูตรทางสถิติที่แสดงถึงความแปรปรวน ความสำคัญของค่าเบี่ยงเบนมาตรฐานในการสำรวจ ค่าเบี่ยงเบนมาตรฐานให้การวัดความน่าเชื่อถือในคำตอบ ในขณะที่คะแนนเฉลี่ยหรือค่าเฉลี่ยอาจให้สรุปอย่างรวดเร็ว ค่าเบี่ยงเบนมาตรฐานจะเพิ่มบริบท มันจะแสดงให้เห็นว่าคำตอบส่วนใหญ่มีการรวมกันอยู่รอบๆ ค่าเฉลี่ยนั้นหรือไม่ หรือถูกกระจายอยู่ในช่วงกว้าง ค่าเบี่ยงเบนมาตรฐานที่น้อยแสดงถึงความสอดคล้อง ขณะที่ค่าที่มากจะชี้ถึงความแปรปรวน ซึ่งอาจบ่งบอกถึงความแตกต่างในการตีความหรือประสบการณ์ การวัดนี้ช่วยให้นักวิจัยและธุรกิจเห็นภาพรวมของข้อมูลสำรวจ ทำให้สามารถระบุพื้นที่ที่ความคิดเห็นแตกต่างกัน และนำไปสู่การปรับปรุงหรือเปลี่ยนแปลงที่มีเป้าหมายในที่สุด การคำนวณค่าเบี่ยงเบนมาตรฐานทีละขั้นตอน พร้อมตัวอย่าง การคำนวณค่าเบี่ยงเบนมาตรฐานอาจดูซับซ้อนในตอนแรก แต่เป็นกระบวนการทีละขั้นตอนที่ง่ายขึ้นเมื่อได้ฝึกฝน เริ่มจากการคำนวณค่าเฉลี่ย (ค่าเฉลี่ย) ของชุดข้อมูลของคุณ จากนั้นให้หักค่าเฉลี่ยออกจากแต่ละจุดข้อมูล สแควร์ผลลัพธ์และหาค่าเฉลี่ยของความแตกต่างที่ถูกสแควร์ในที่สุด ให้เอารากที่สองของค่าเฉลี่ยนั้นเพื่อหาค่าเบี่ยงเบนมาตรฐาน เริ่มต้นด้วยการใช้สูตรดังนี้: 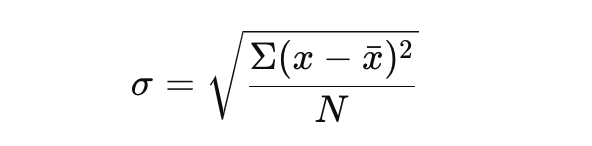สูตรนี้ให้ภาพรวมที่ชัดเจนเกี่ยวกับความแปรปรวนในชุดข้อมูลของคุณ สมมติว่าคุณได้ทำการสำรวจถามลูกค้า 5 คน ให้คะแนนความพึงพอใจกับบริการของคุณในระดับ 1 ถึง 10 คำตอบคือ: 7, 8, 6, 9, 10 ตอนนี้มาคำนวณค่าเบี่ยงเบนมาตรฐานสำหรับชุดข้อมูลนี้กัน: ขั้นตอนที่ 1: หาค่าเฉลี่ย เพื่อหาค่าเฉลี่ย ให้นำข้อมูลทั้งหมดมาบวกกันแล้วหารด้วยจำนวนคำตอบ 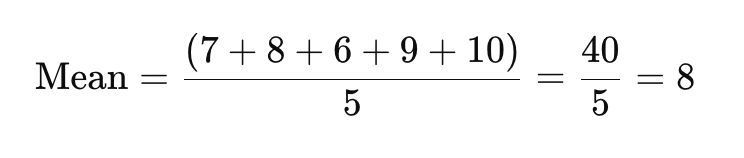ค่าเฉลี่ยของคะแนนความพึงพอใจในที่นี้คือ 8 ขั้นตอนที่ 2: หักค่าเฉลี่ยออกจากแต่ละจุดข้อมูลและสแควร์ผลลัพธ์ ถัดไป สำหรับคะแนนแต่ละคะแนน ให้นำค่าเฉลี่ย (8) หักออกแล้วสแควร์ผลลัพธ์ เพื่อให้ค่าลบไม่มีและเน้นความเบี่ยงเบน 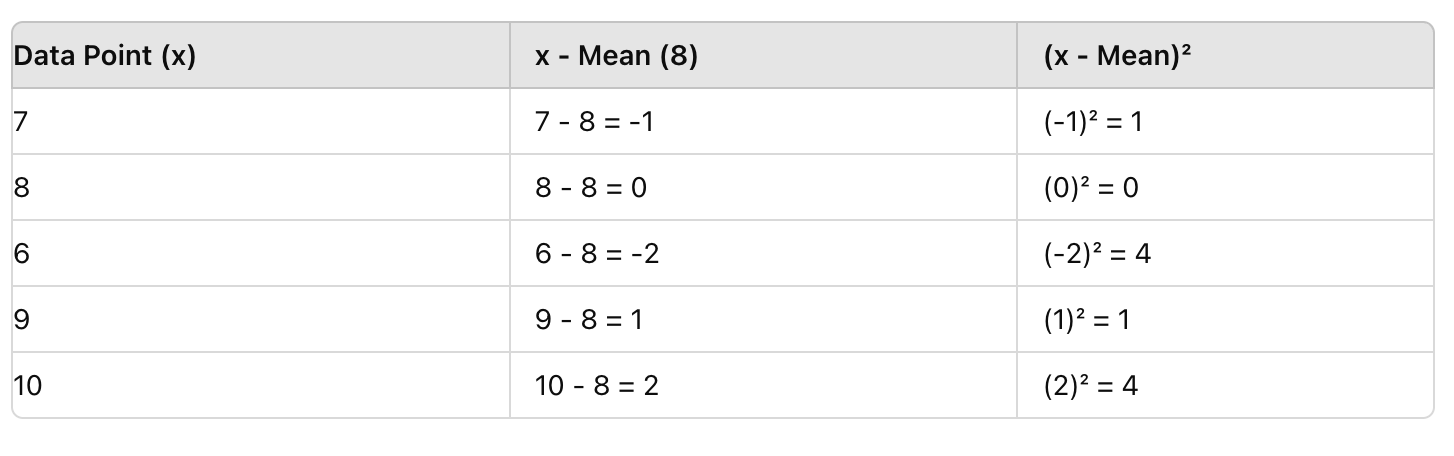ขั้นตอนที่ 3: หาค่าเฉลี่ยของความแตกต่างที่ถูกสแควร์ ตอนนี้ ให้นำความแตกต่างที่ถูกสแควร์มาบวกกันแล้วหารด้วยจำนวนข้อมูลเพื่อหาความแปรปรวน 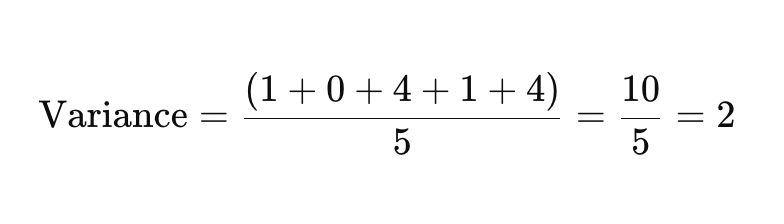ขั้นตอนที่ 4: เอารากที่สองของความแปรปรวน ในที่สุด ให้นำรากที่สองของความแปรปรวนมาเพื่อหาค่าเบี่ยงเบนมาตรฐาน ในตัวอย่างนี้ ค่าเบี่ยงเบนมาตรฐานอยู่ที่ประมาณ 1.41 ซึ่งหมายความว่าส่วนใหญ่คะแนนความพึงพอใจของลูกค้าอยู่ภายใน 1.41 คะแนนจากค่าเฉลี่ย (8) เนื่องจากค่าเบี่ยงเบนมาตรฐานค่อนข้างเล็ก คะแนนจึงใกล้เคียงกับค่าเฉลี่ย แสดงถึงความสอดคล้องในความคิดเห็น หากค่าเบี่ยงเบนมาตรฐานใหญ่ขึ้น เช่น 3 หรือ 4 จะบ่งบอกถึงการกระจายของคำตอบที่กว้างขึ้น โดยมีลูกค้าบางคนพอใจมากหรือน้อยกว่าคนอื่น ค่าเบี่ยงเบนมาตรฐานใน Excel คู่มือทีละขั้นตอนในการใช้ Excel สำหรับค่าเบี่ยงเบนมาตรฐาน Microsoft Excel หรือ Google Sheets เป็นเครื่องมือที่สะดวกที่สุดในการคำนวณค่าเบี่ยงเบนมาตรฐาน นี่คือวิธีการ: ป้อนข้อมูลของคุณในคอลัมน์ เลือกเซลล์ว่างที่คุณต้องการแสดงผลลัพธ์ ใช้สูตร =STDEV.P() สำหรับค่าเบี่ยงเบนมาตรฐานตามประชากร หรือ =STDEV.S() สำหรับค่าเบี่ยงเบนมาตรฐานของตัวอย่าง ไฮไลท์ข้อมูลของคุณ, กด Enter, และ Excel จะคำนวณผลลัพธ์ทันที Excel ช่วยให้กระบวนการนี้อัตโนมัติ ประหยัดเวลาและลดโอกาสเกิดข้อผิดพลาดจากการกรอกข้อมูลด้วยตนเอง การส่งออกข้อมูล LimeSurvey ไปยัง Excel ด้วย LimeSurvey คุณสามารถส่งออกข้อมูลการสำรวจของคุณไปยัง Excel โดยตรงเพื่อวิเคราะห์ผลลัพธ์เพิ่มเติม ทำได้โดย: ไปที่ส่วนผลลัพธ์ใน LimeSurvey เลือกตัวเลือกการส่งออกและเลือก Excel เป็นรูปแบบ เมื่อส่งออกเสร็จแล้ว ให้ใช้ฟังก์ชันทางสถิติของ Excel รวมถึงค่าเบี่ยงเบนมาตรฐาน เพื่อเข้าใจข้อมูลของคุณได้ลึกซึ้งขึ้น โดยการรวมความสามารถในการเก็บข้อมูลของ LimeSurvey กับเครื่องมือวิเคราะห์ของ Excel คุณสามารถตีความและดำเนินการข้อมูลสำรวจของคุณได้อย่างมีประสิทธิภาพ เข้าใจค่าเบี่ยงเบนมาตรฐาน ค่าเบี่ยงเบนมาตรฐานและข้อผิดพลาดมาตรฐาน ค่าเบี่ยงเบนมาตรฐานและข้อผิดพลาดมาตรฐานมีความเกี่ยวข้องกัน แต่ทำหน้าที่ต่างกัน ค่าเบี่ยงเบนมาตรฐานใช้วัดการกระจายของจุดข้อมูลแต่ละจุด ในขณะที่ข้อผิดพลาดมาตรฐานใช้วัดความแม่นยำของค่าเฉลี่ยตัวอย่างเมื่อเปรียบเทียบกับค่าเฉลี่ยประชากรจริง ในการสำรวจ ค่าเบี่ยงเบนมาตรฐานจะช่วยให้คุณเข้าใจความแปรปรวนในคำตอบ ในขณะที่ข้อผิดพลาดมาตรฐานใช้ในการประมาณค่าความใกล้เคียงของค่าเฉลี่ยตัวอย่างกับค่าเฉลี่ยประชากรจริง ค่าเบี่ยงเบนมาตรฐานและความแปรปรวน ความแปรปรวนเป็นอีกหนึ่งการวัดการกระจายของข้อมูล และเป็นสแควร์ของค่าเบี่ยงเบนมาตรฐาน แม้ว่าอาจช่วยในการวัดขนาดของความแปรปรวน แต่ค่าเบี่ยงเบนมาตรฐานจะเข้าใจง่ายกว่าเพราะแสดงในหน่วยเดียวกับข้อมูลต้นฉบับ ตัวอย่างเช่น หากคุณกำลังวัดคะแนนความพึงพอใจ ค่าเบี่ยงเบนมาตรฐานจะให้ความเข้าใจที่ชัดเจนว่า ความแตกต่างระหว่างคำตอบมีมากน้อยเพียงใด การตีความผลลัพธ์ค่าเบี่ยงเบนมาตรฐาน เมื่อคุณได้คำนวณค่าเบี่ยงเบนมาตรฐานแล้ว คุณสามารถใช้มันเพื่อตีความความสอดคล้องของคำตอบในการสำรวจ ค่าเบี่ยงเบนมาตรฐานต่ำหมายถึงผู้ตอบส่วนใหญ่มีความคิดเห็นที่ตรงกัน ในขณะที่ค่าเบี่ยงเบนมาตรฐานสูงแสดงถึงความคิดเห็นที่แตกต่าง ตัวอย่างเช่น สมมติว่าคุณได้สำรวจพนักงาน 100 คนเกี่ยวกับความพึงพอใจในงาน โดยให้คะแนนในระดับ 1 ถึง 10 หากคำตอบส่วนใหญ่อยู่ใกล้เคียงกับ 8 โดยมีค่าเบี่ยงเบนมาตรฐานน้อย แสดงถึงความพึงพอใจทั่วไป อย่างไรก็ตาม หากคะแนนอยู่ในช่วง 4 ถึง 10 ค่าเบี่ยงเบนมาตรฐานที่ใหญ่ขึ้นแสดงให้เห็นว่าความคิดเห็นแตกต่างกันมากขึ้น และคุณอาจต้องสอบสวนเพิ่มเติม การประยุกต์ใช้ค่าเบี่ยงเบนมาตรฐานในทางปฏิบัติ ปรับปรุงคำถามในการสำรวจ: หากคุณสังเกตเห็นค่าเบี่ยงเบนมาตรฐานใหญ่ในคำถามสำรวจเฉพาะ อาจบ่งชี้ว่าคำถามนั้นคลุมเครือหรือไม่ชัดเจนสำหรับผู้ตอบ การปรับปรุงการใช้คำสามารถช่วยให้รวบรวมข้อมูลที่ถูกต้องมากขึ้นในการสำรวจในอนาคต การตัดสินใจโดยอิงจากข้อมูล: ค่าเบี่ยงเบนมาตรฐานช่วยให้คุณตัดสินใจได้ดียิ่งขึ้นโดยนำเสนอรูปแบบในข้อมูลสำรวจของคุณ ตัวอย่างเช่น หากความคิดเห็นแตกต่างกันมาก คุณสามารถแบ่งกลุ่มกลุ่มเป้าหมายและปรับคำตอบให้เหมาะสมได้ การรับประกันความถูกต้องในค่าเบี่ยงเบนมาตรฐาน ข้อมูลที่ขาดหายไป: ข้อมูลที่ขาดหายไปสามารถบิดเบือนการคำนวณค่าเบี่ยงเบนมาตรฐาน การหลีกเลี่ยงความไม่ถูกต้อง ควรบริหารจัดการข้อมูลที่ขาดโดยการไม่รวมคำตอบที่ไม่สมบูรณ์หรือใช้เทคนิคการประมาณค่า หลีกเลี่ยงค่าวิคฤต: การตรวจสอบข้อมูลของคุณทำให้มั่นใจในความถูกต้อง การตรวจสอบความผิดพลาดหรือค่าวิคฤตเป็นสิ่งสำคัญ แม้แต่การป้อนข้อมูลที่ไม่ถูกต้องเพียงรายการเดียวสามารถเปลี่ยนแปลงผลลัพธ์ของคุณได้อย่างมีนัยสำคัญ การใช้เครื่องมือสำรวจของ LimeSurvey ช่วยให้คุณเก็บข้อมูลที่ถูกต้องและใช้ได้ซึ่งสะท้อนให้เห็นถึงความแปรปรวนที่แท้จริง เริ่มต้นด้วยการเข้าใจค่าเบี่ยงเบนมาตรฐาน คุณจะได้ข้อมูลเชิงลึกที่มีประสิทธิภาพในการสำรวจผลลัพธ์ของคุณ ซึ่งช่วยให้คุณไม่เพียงแต่ตีความข้อมูลได้ดีขึ้น แต่ยังสามารถตัดสินใจได้ดียิ่งขึ้นจากการเข้าใจลึกซึ้งว่าผู้ตอบมีความรู้สึกอย่างไร ทำอะไร หรือคิดอย่างไร หลังจากกำหนดค่าเบี่ยงเบนมาตรฐานแล้ว LimeSurvey ช่วยให้คุณปรับปรุงคำถามของคุณได้ ดังนั้นคุณสามารถใช้ประโยชน์สูงสุดจากการสำรวจและข้อมูลของคุณได้ ลองใช้วันนี้เลย!