Deviasi standar: semua yang perlu anda ketahui untuk survei

Bayangkan Anda menjalankan survei kepuasan pelanggan untuk jaringan kafe yang populer. Anda mengharapkan sebagian besar pelanggan memberikan penilaian tinggi untuk kopi Anda—setelah semua, kafe Anda bangga dengan pengendalian kualitas dan layanan yang baik. Namun, saat melihat hasilnya, penilaian sangat bervariasi. Beberapa pelanggan memberikan ulasan positif, sementara yang lain tampaknya memiliki pengalaman buruk. Apa yang terjadi? Di sinilah deviasi standar membantu dalam mengkuantifikasi data Anda, memungkinkan Anda memahami apakah tanggapan yang diterima saling terkait erat atau sangat bervariasi. Dengan metode ini, Anda dapat mengungkap apakah beberapa skor rendah adalah data pencilan, atau apakah penawaran merek Anda benar-benar tidak konsisten. Apa itu Deviasi Standar? Pada dasarnya, deviasi standar mengukur seberapa menyebar nilai-nilai dalam dataset. Ini memberi tahu Anda seberapa banyak tanggapan individu menyimpang dari rata-rata, membantu Anda memahami apakah data Anda konsisten atau memiliki variabilitas yang signifikan. Dalam analisis survei, deviasi standar memberikan wawasan lebih dalam tentang bagaimana orang merespons, menjadikannya alat yang berharga untuk menginterpretasi hasil. Misalnya, jika semua pelanggan Anda memberikan penilaian 8 atau 9 dari 10 untuk layanan Anda, Anda akan mendapatkan deviasi standar yang kecil, artinya hasilnya cukup konsisten. Di sisi lain, jika beberapa memberi nilai 2 dan yang lain 10, deviasi standarnya akan jauh lebih besar, menunjukkan pendapat yang lebih beragam. Simbol untuk deviasi standar adalah “σ” (sigma kecil) untuk deviasi standar populasi, dan “sss” untuk deviasi standar sampel. Ini adalah singkatan yang digunakan dalam persamaan statistik dan rumus untuk menunjukkan variabilitas. Pentingnya Deviasi Standar dalam Survei Deviasi standar menyediakan ukuran keandalan dalam tanggapan. Sementara skor rata-rata mungkin memberikan ringkasan cepat, deviasi standar memberikan konteks. Ini menunjukkan apakah sebagian besar tanggapan terpusat di sekitar rata-rata itu atau menyebar di rentang yang luas. Deviasi standar yang kecil menunjukkan konsistensi, sedangkan yang besar menunjuk pada variabilitas—yang dapat menunjukkan perbedaan dalam interpretasi atau pengalaman. Pengukuran ini memungkinkan peneliti dan bisnis untuk melihat lebih dalam ke permukaan data survei, membantu mereka mengidentifikasi area di mana pendapat berbeda, dan akhirnya membimbing perbaikan atau perubahan yang lebih terarah. Menghitung Deviasi Standar Langkah demi Langkah, dengan Contoh Menghitung deviasi standar mungkin terlihat kompleks pada awalnya, tetapi itu adalah proses langkah demi langkah yang semakin mudah dengan praktik. Pertama, hitung rata-rata (mean) dari dataset Anda. Kemudian, kurangi rata-rata dari setiap titik data, kuadratkan hasilnya, dan cari rata-rata dari perbedaan kuadrat ini. Akhirnya, ambil akar kuadrat dari rata-rata ini untuk mendapatkan deviasi standar. 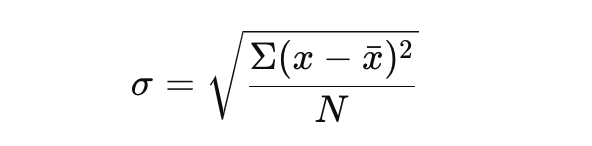Mari kita mulai dengan menggunakan rumus berikut: Rumus ini memberikan gambaran yang jelas tentang variabilitas dalam dataset Anda. Misalkan Anda melakukan survei meminta 5 pelanggan untuk menilai kepuasan mereka terhadap layanan Anda pada skala 1 sampai 10. Tanggapan yang diberikan adalah: 7, 8, 6, 9, 10. Sekarang, mari kita hitung deviasi standar untuk dataset ini: Langkah 1: Temukan Rata-rata (Mean) Untuk menemukan rata-rata, tambahkan semua titik data bersama dan bagi dengan jumlah tanggapan. 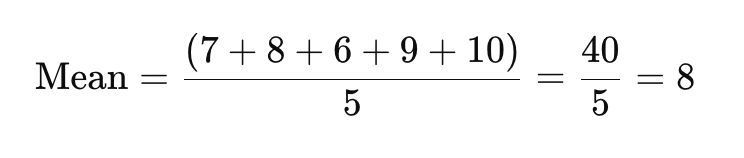Skor kepuasan rata-rata di sini adalah 8. Langkah 2: Kurangi Rata-rata dari Setiap Titik Data dan Kuadratkan Hasilnya Selanjutnya, untuk setiap skor, kurangi rata-rata (8), kemudian kuadratkan hasilnya. Ini menghapus nilai negatif dan menyoroti penyimpangan. 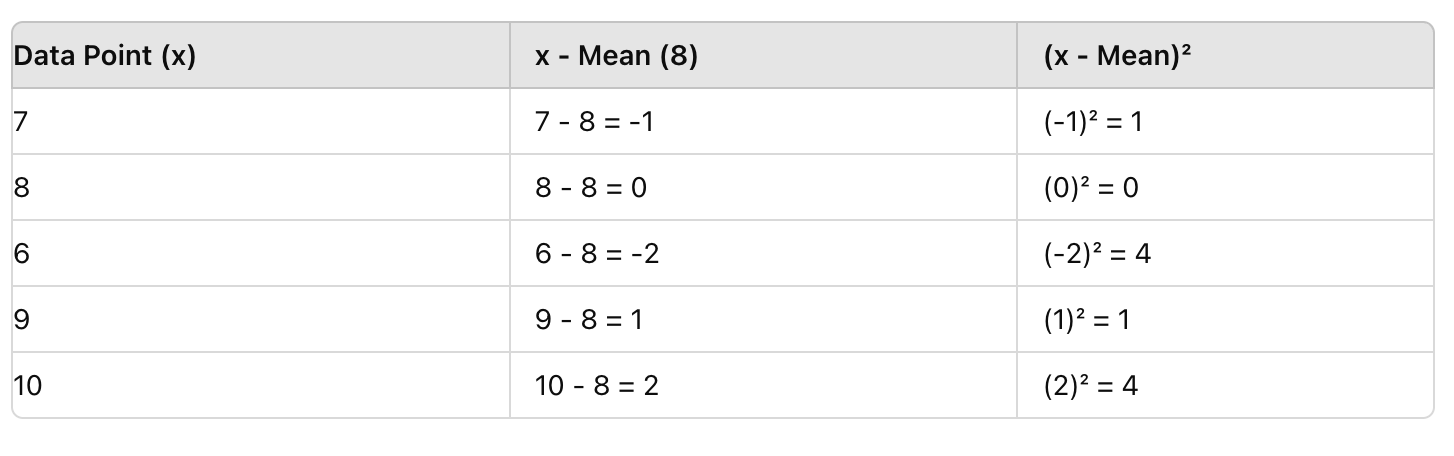Langkah 3: Temukan Rata-rata dari Perbedaan Kuadrat Sekarang, jumlahkan perbedaan kuadrat dan bagi dengan jumlah titik data untuk menemukan varians. 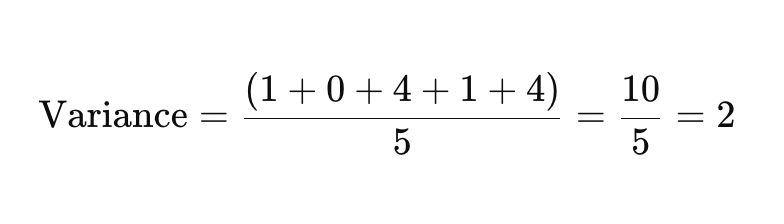Langkah 4: Ambil Akar Kuadrat dari Varians Terakhir, ambil akar kuadrat dari varians untuk menemukan deviasi standar. Dalam contoh ini, deviasi standar adalah sekitar 1,41. Ini berarti sebagian besar skor kepuasan pelanggan berada dalam jarak 1,41 poin dari skor rata-rata (8). Karena deviasi standar relatif kecil, penilaian cukup dekat dengan rata-rata, menunjukkan konsistensi dalam umpan balik. Jika deviasi standar lebih besar, misalnya 3 atau 4, itu akan menunjukkan penyebaran tanggapan yang lebih luas, dengan beberapa pelanggan jauh lebih atau kurang puas dibandingkan yang lain. Deviasi Standar di Excel Panduan Langkah demi Langkah Menggunakan Excel untuk Deviasi Standar Microsoft Excel atau Google Sheets adalah salah satu alat paling praktis untuk menghitung deviasi standar. Begini caranya: Masukkan data Anda ke dalam sebuah kolom. Pilih sel kosong tempat Anda ingin hasilnya muncul. Gunakan rumus =STDEV.P() untuk deviasi standar populasi atau =STDEV.S() untuk deviasi standar sampel. Sorot data Anda, tekan Enter, dan Excel akan segera menghitung hasilnya. Excel mengotomatiskan proses ini, menghemat waktu Anda dan mengurangi potensi kesalahan manual. Ekspor Data LimeSurvey ke Excel Dengan LimeSurvey, Anda dapat mengekspor data survei Anda langsung ke Excel untuk menganalisis hasil Anda lebih lanjut. Untuk melakukannya: navigasikan ke bagian hasil di LimeSurvey. Pilih opsi ekspor dan pilih Excel sebagai formatnya. Setelah diekspor, gunakan fungsi statistik Excel, termasuk deviasi standar, untuk mendapatkan pemahaman yang lebih dalam tentang data Anda. Dengan menggabungkan kemampuan pengumpulan data LimeSurvey dengan alat analisis Excel, Anda dapat dengan efisien menginterpretasikan dan bertindak berdasarkan hasil survei Anda. Memahami Deviasi Standar Deviasi Standar vs. Kesalahan Standar Deviasi standar dan kesalahan standar saling terkait, tetapi memiliki tujuan yang berbeda. Deviasi standar mengukur penyebaran titik data individu, sementara kesalahan standar mengukur ketepatan rata-rata sampel dibandingkan dengan rata-rata populasi yang sebenarnya. Dalam survei, deviasi standar membantu Anda memahami variabilitas dalam tanggapan, sementara kesalahan standar berguna untuk memperkirakan seberapa dekat rata-rata sampel Anda dengan rata-rata populasi yang sebenarnya. Deviasi Standar vs. Varians Varians adalah ukuran lain dari penyebaran data, dan merupakan kuadrat dari deviasi standar. Sementara varians membantu mengukur magnitudo variabilitas, deviasi standar lebih mudah diinterpretasikan karena dinyatakan dalam satuan yang sama dengan data asli Anda. Misalnya, jika Anda mengukur skor kepuasan, deviasi standar akan memberikan pemahaman intuitif tentang seberapa banyak tanggapan berbeda dari rata-rata. Menginterpretasi Hasil Deviasi Standar Setelah Anda menghitung deviasi standar, Anda dapat menggunakannya untuk menginterpretasikan konsistensi tanggapan survei Anda. Deviasi standar yang rendah berarti bahwa responden umumnya setuju, sedangkan deviasi standar yang tinggi menandakan pendapat yang bervariasi. Misalnya, bayangkan Anda mensurvei 100 karyawan tentang kepuasan kerja mereka pada skala 1 sampai 10. Jika sebagian besar tanggapan terpusat di sekitar 8, dengan deviasi standar yang kecil, itu menunjukkan kepuasan umum. Namun, jika penilaian berkisar dari 4 hingga 10, deviasi standar yang lebih besar menunjukkan bahwa pendapat lebih terbagi, dan Anda mungkin perlu menyelidiki lebih lanjut. Aplikasi Praktis Deviasi Standar Meningkatkan Pertanyaan Survei: Jika Anda melihat deviasi standar yang besar untuk pertanyaan survei tertentu, itu mungkin menunjukkan bahwa pertanyaan tersebut ambigu atau tidak dipahami dengan baik oleh responden. Memperbaiki kata-kata dapat membantu mengumpulkan data yang lebih akurat di survei mendatang. Pengambilan Keputusan Berbasis Data: Deviasi standar membantu Anda membuat keputusan yang lebih tepat dengan mengungkap pola dalam data survei Anda. Misalnya, jika umpan balik sangat bervariasi, Anda dapat membagi audiens Anda dan menyesuaikan respons sesuai kebutuhan. Memastikan Akurasi dalam Deviasi Standar Data yang Hilang: Data yang hilang dapat mendistorsi perhitungan deviasi standar Anda. Untuk menghindari ketidakakuratan, baik perhitungkan data yang hilang dengan mengecualikan tanggapan yang tidak lengkap atau gunakan teknik imputasi. Menjauhi Pencilan: Memeriksa data Anda untuk kesalahan atau pencilan sangat penting. Bahkan satu entri yang salah dapat secara signifikan mengubah hasil Anda. Menggunakan alat survei LimeSurvey dapat membantu Anda mengumpulkan data yang akurat dan dapat digunakan yang mencerminkan variabilitas yang sebenarnya. Dengan memulai pemahaman tentang deviasi standar, Anda akan membuka wawasan yang kuat ke dalam hasil survei Anda. Ini memungkinkan Anda tidak hanya menginterpretasikan data lebih efektif, tetapi juga membuat keputusan yang lebih baik berdasarkan pemahaman yang lebih dalam tentang bagaimana responden Anda merasa, bertindak, atau berpikir. Setelah menentukan deviasi standar, LimeSurvey memungkinkan Anda meningkatkan pertanyaan Anda, sehingga Anda bisa memanfaatkan survei dan data dengan sebaik-baiknya. Coba sekarang juga!