Desviación estándar: todo lo que necesitas saber para encuestas.

Imagina que realizas una encuesta de satisfacción del cliente para una popular cadena de cafés. Esperas que la mayoría de los clientes califiquen el café altamente, ya que tu café se enorgullece del control de calidad y el excelente servicio. Pero al revisar los resultados, las calificaciones son muy variadas. Algunos clientes dan reseñas muy positivas, mientras que otros parecen haber tenido una mala experiencia. ¿Qué está pasando? Aquí es donde la desviación estándar ayuda a cuantificar tus datos, permitiéndote entender si las respuestas que recibes están alineadas o si varían drásticamente. Con este método, puedes descubrir si aquellas pocas calificaciones bajas son puntos atípicos o si las ofertas de tu marca son realmente inconsistentes. ¿Qué es la Desviación Estándar? En esencia, la desviación estándar mide cuán dispersos están los valores en un conjunto de datos. Te indica cuánto se desvían las respuestas individuales de la media, ayudándote a entender si tus datos son consistentes o presentan variabilidad significativa. En el análisis de encuestas, la desviación estándar proporciona una visión más profunda de las respuestas de las personas, convirtiéndose en una herramienta valiosa para interpretar resultados. Por ejemplo, si todos tus clientes califican tu servicio con un 8 o 9 de 10, tendrías una pequeña desviación estándar, lo que significa que los resultados son bastante consistentes. Por otro lado, si algunos lo califican con un 2 y otros con un 10, la desviación estándar será mucho mayor, señalando opiniones más diversas. El símbolo de la desviación estándar es “σ” (sigma minúscula) para la desviación estándar poblacional y “sss” para la desviación estándar muestral. Es una abreviatura utilizada en ecuaciones y fórmulas estadísticas para denotar variabilidad. La Importancia de la Desviación Estándar en Encuestas La desviación estándar proporciona una medida de fiabilidad en las respuestas. Aunque la media (o promedio) te dé un resumen rápido, la desviación estándar añade contexto. Muestra si la mayoría de las respuestas están agrupadas alrededor de esa media o si están distribuidas en un amplio rango. Una pequeña desviación estándar sugiere consistencia, mientras que una grande indica variabilidad, lo que puede señalar diferencias en la interpretación o experiencia. Esta medida permite a los investigadores y empresas ver más allá de la superficie de los datos de la encuesta, ayudándoles a identificar áreas donde las opiniones divergen, guiando así mejoras o cambios más específicos. Cálculo de la Desviación Estándar Paso a Paso, con un Ejemplo Calcular la desviación estándar puede parecer complejo al principio, pero es un proceso paso a paso que se vuelve más fácil con la práctica. Primero, calcula la media de tu conjunto de datos. Luego, resta la media de cada punto de datos, eleva el resultado al cuadrado y encuentra la media de estas diferencias al cuadrado. Finalmente, toma la raíz cuadrada de esta media para obtener la desviación estándar. 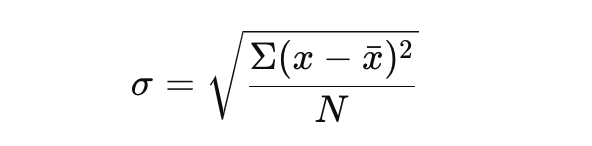Comencemos usando la siguiente fórmula: Esta fórmula te ofrece una imagen clara de la variabilidad en tu conjunto de datos. Supongamos que realizaste una encuesta pidiendo a 5 clientes que calificaran su satisfacción con tu servicio en una escala del 1 al 10. Las respuestas fueron: 7, 8, 6, 9, 10. Ahora, calculemos la desviación estándar para este conjunto de datos: Paso 1: Encontrar la Media Para encontrar la media, suma todos los puntos de datos y divide por el número de respuestas. 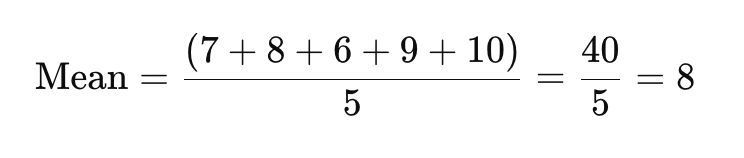La media de satisfacción aquí es 8. Paso 2: Restar la Media de Cada Punto de Datos y Elevar el Resultado al Cuadrado A continuación, para cada calificación, resta la media (8), y luego eleva el resultado al cuadrado. Esto elimina los valores negativos y resalta las desviaciones. 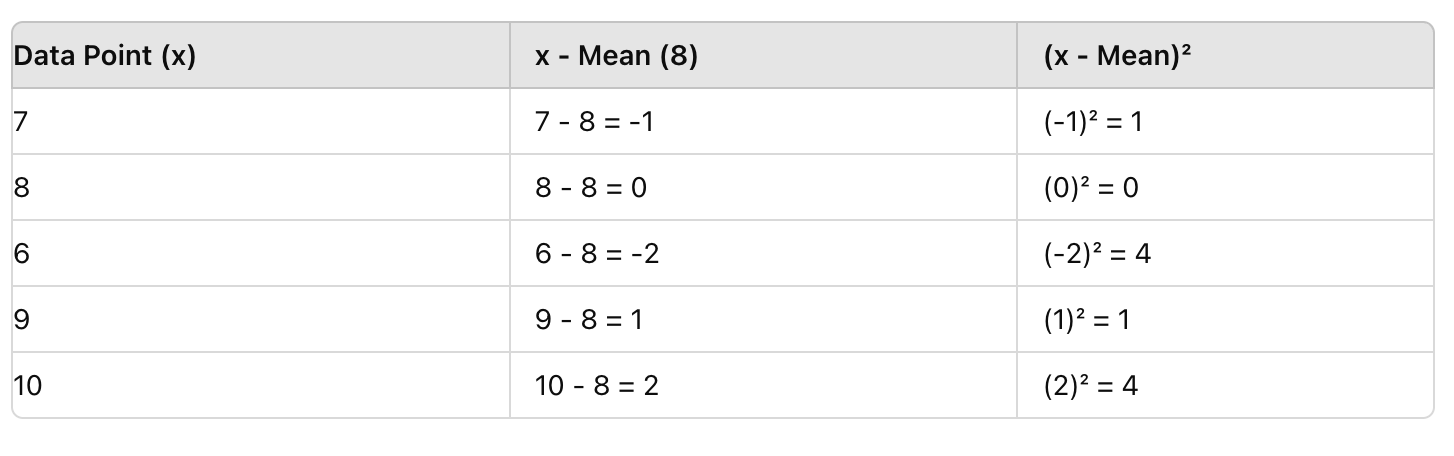Paso 3: Encontrar la Media de las Diferencias al Cuadrado Ahora, suma las diferencias al cuadrado y divide por el número de puntos de datos para encontrar la varianza. 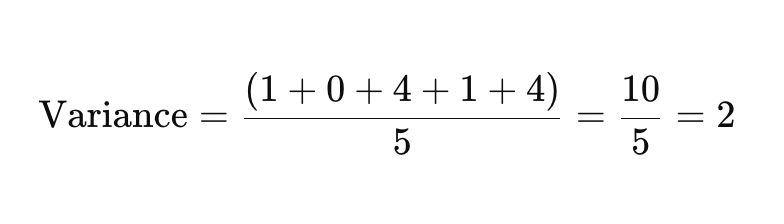Paso 4: Tomar la Raíz Cuadrada de la Varianza Finalmente, toma la raíz cuadrada de la varianza para encontrar la desviación estándar. En este ejemplo, la desviación estándar es aproximadamente 1.41. Esto significa que la mayoría de las calificaciones de satisfacción del cliente están dentro de 1.41 puntos de la media (8). Dado que la desviación estándar es relativamente pequeña, las calificaciones están bastante cerca del promedio, indicando consistencia en los comentarios. Si la desviación estándar fuera mayor, digamos 3 o 4, sugeriría una mayor dispersión de respuestas, con algunos clientes mucho más o menos satisfechos que otros. Desviación Estándar en Excel Guía Paso a Paso para Usar Excel en Desviación Estándar Microsoft Excel o Google Sheets son herramientas muy convenientes para calcular la desviación estándar. Así es como hacerlo: Ingresa tus datos en una columna. Selecciona una celda vacía donde deseas que aparezca el resultado. Usa la fórmula =STDEV.P() para la desviación estándar poblacional o =STDEV.S() para la desviación estándar muestral. Resalta tus datos, presiona Enter y Excel calculará instantáneamente el resultado. Excel automatiza el proceso, ahorrándote tiempo y reduciendo la posibilidad de errores manuales. Exportando Datos de LimeSurvey a Excel Con LimeSurvey, puedes exportar los datos de tu encuesta directamente a Excel para analizar los resultados. Para hacerlo: Navega a la sección de resultados en LimeSurvey. Selecciona la opción de exportar y elige Excel como formato. Una vez exportado, utiliza las funciones estadísticas de Excel, incluida la desviación estándar, para obtener una comprensión más profunda de tus datos. Al combinar las capacidades de recolección de datos de LimeSurvey con las herramientas de análisis de Excel, puedes interpretar y actuar sobre los resultados de tu encuesta de manera eficiente. Entendiendo la Desviación Estándar Desviación Estándar vs. Error Estándar La desviación estándar y el error estándar están relacionados, pero sirven para diferentes propósitos. La desviación estándar mide la dispersión de los puntos de datos individuales, mientras que el error estándar mide la precisión de la media muestral en comparación con la verdadera media poblacional. En encuestas, la desviación estándar ayuda a entender la variabilidad en las respuestas, mientras que el error estándar es útil para estimar cuán cerca está tu media muestral de la verdadera media poblacional. Desviación Estándar vs. Varianza La varianza es otra medida de dispersión de datos y es el cuadrado de la desviación estándar. Mientras que la varianza ayuda a cuantificar la magnitud de la variabilidad, la desviación estándar es más fácil de interpretar porque se expresa en las mismas unidades que tus datos originales. Por ejemplo, si estás midiendo puntuaciones de satisfacción, la desviación estándar proporcionará una comprensión intuitiva de cuánto difieren las respuestas del promedio. Interpretando Resultados de la Desviación Estándar Una vez calculada la desviación estándar, puedes usarla para interpretar la consistencia de las respuestas de tu encuesta. Una baja desviación estándar significa que los encuestados están generalmente de acuerdo, mientras que una alta desviación estándar indica opiniones variadas. Por ejemplo, imagina que encuestaste a 100 empleados sobre su satisfacción laboral en una escala del 1 al 10. Si la mayoría de las respuestas están agrupadas alrededor del 8, con una baja desviación estándar, sugiere satisfacción general. Sin embargo, si las calificaciones varían de 4 a 10, la mayor desviación estándar muestra que las opiniones están más divididas, y puede que necesites investigar más. Aplicaciones Prácticas de la Desviación Estándar Mejorando Preguntas de Encuesta: Si notas una gran desviación estándar para una pregunta específica, podría indicar que la pregunta es ambigua o no está bien comprendida por los encuestados. Refinar la redacción puede ayudar a recopilar datos más precisos en futuras encuestas. Tomando Decisiones Basadas en Datos: La desviación estándar te ayuda a tomar decisiones más informadas al revelar patrones en tus datos de encuestas. Por ejemplo, si los comentarios son muy variables, puedes segmentar tu audiencia y adaptar las respuestas en consecuencia. Asegurando Precisión en la Desviación Estándar Datos Faltantes: Los datos faltantes pueden distorsionar tu cálculo de desviación estándar. Para evitar inexactitudes, puedes eliminar respuestas incompletas o utilizar técnicas de imputación. Evitando Atípicos: Verificar tus datos en busca de errores o puntos atípicos es esencial. Incluso una entrada incorrecta puede alterar significativamente tus resultados. Usar las herramientas de encuesta de LimeSurvey puede ayudarte a recopilar datos precisos que reflejen la variabilidad real. Al comenzar con un entendimiento de la desviación estándar, desbloquearás poderosas perspectivas sobre los resultados de tu encuesta. Esto te permitirá interpretar los datos de manera más efectiva y tomar mejores decisiones basadas en una comprensión más profunda de cómo se sienten, actúan o piensan tus encuestados. Después de determinar la desviación estándar, LimeSurvey te permite mejorar tus preguntas, para que puedas aprovechar al máximo tu encuesta y tus datos. ¡Pruébalo hoy!