Desvio padrão: tudo que você precisa saber para pesquisas

Imagine que você conduz uma pesquisa de satisfação do cliente para uma popular cadeia de cafeterias. Espera que a maioria dos clientes classifique o café muito bem—afinal, sua cafeteria se orgulha de controle de qualidade e excelente serviço. Mas ao olhar os resultados, as classificações estão desordenadas. Alguns clientes dão comentários excelentes, enquanto outros parecem ter tido uma experiência ruim. O que está acontecendo? Aqui é onde o desvio padrão ajuda a quantificar seus dados, permitindo entender se as respostas são alinhadas ou se variam muito. Com este método, você pode descobrir se aquelas algumas pontuações baixas são outliers ou se as ofertas da sua marca são realmente inconsistentes. O que é Desvio Padrão? Em essência, o desvio padrão mede o quão dispersos estão os valores em um conjunto de dados. Ele indica quanto as respostas individuais se desviam da média, ajudando a entender se seus dados são consistentes ou apresentam variabilidade significativa. Na análise de pesquisas, o desvio padrão fornece insights mais profundos sobre como as pessoas respondem, tornando-se uma ferramenta valiosa para a interpretação dos resultados. Por exemplo, se todos os seus clientes classificam seu serviço como 8 ou 9 de 10, você teria um pequeno desvio padrão, indicando que os resultados são bastante consistentes. Por outro lado, se alguns classificam como 2 e outros como 10, o desvio padrão será muito maior, sinalizando opiniões mais diversas. O símbolo para desvio padrão é “σ” (sigma minúsculo) para o desvio padrão populacional, e “sss” para o desvio padrão amostral. É uma abreviação utilizada em equações e fórmulas estatísticas para denotar variabilidade. A Importância do Desvio Padrão em Pesquisas O desvio padrão fornece uma medida de confiabilidade nas respostas. Enquanto a média pode oferecer um resumo rápido, o desvio padrão adiciona contexto. Ele mostra se a maioria das respostas está agrupada em torno da média ou se estão espalhadas em uma ampla faixa. Um pequeno desvio padrão sugere consistência, enquanto um grande indica variabilidade—o que pode indicar diferenças de interpretação ou experiência. Essa medida permite que pesquisadores e empresas vejam além da superfície dos dados da pesquisa, ajudando a identificar áreas onde as opiniões divergem, e, em última análise, orientando melhorias ou mudanças mais direcionadas. Calculando o Desvio Padrão Passo a Passo, com um Exemplo Calcular o desvio padrão pode parecer complexo à primeira vista, mas é um processo passo a passo que se torna mais fácil com prática. Primeiro, calcule a média do seu conjunto de dados. Em seguida, subtraia a média de cada ponto de dados, eleve o resultado ao quadrado e encontre a média dessas diferenças ao quadrado. Por fim, tire a raiz quadrada dessa média para obter o desvio padrão. 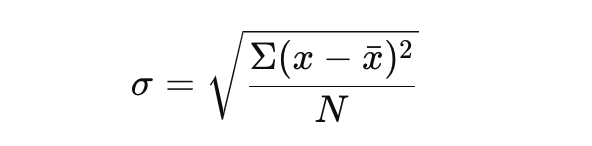Vamos começar usando a seguinte fórmula: Essa fórmula lhe dá uma imagem clara da variabilidade em seu conjunto de dados. Digamos que você conduziu uma pesquisa pedindo a 5 clientes para avaliar sua satisfação com seu serviço em uma escala de 1 a 10. As respostas foram: 7, 8, 6, 9, 10. Agora, vamos calcular o desvio padrão para este conjunto de dados: Passo 1: Encontrar a Média Para encontrar a média, some todos os pontos de dados e divida pelo número de respostas. 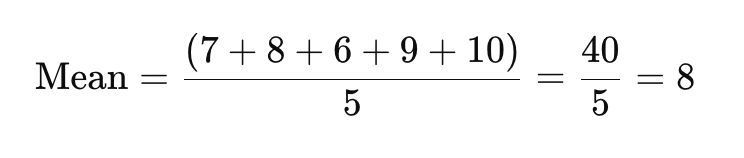A média aqui é 8. Passo 2: Subtrair a Média de Cada Ponto de Dados e Elevar o Resultado ao Quadrado Em seguida, para cada pontuação, subtraia a média (8) e eleve o resultado ao quadrado. Isso remove valores negativos e destaca os desvios. 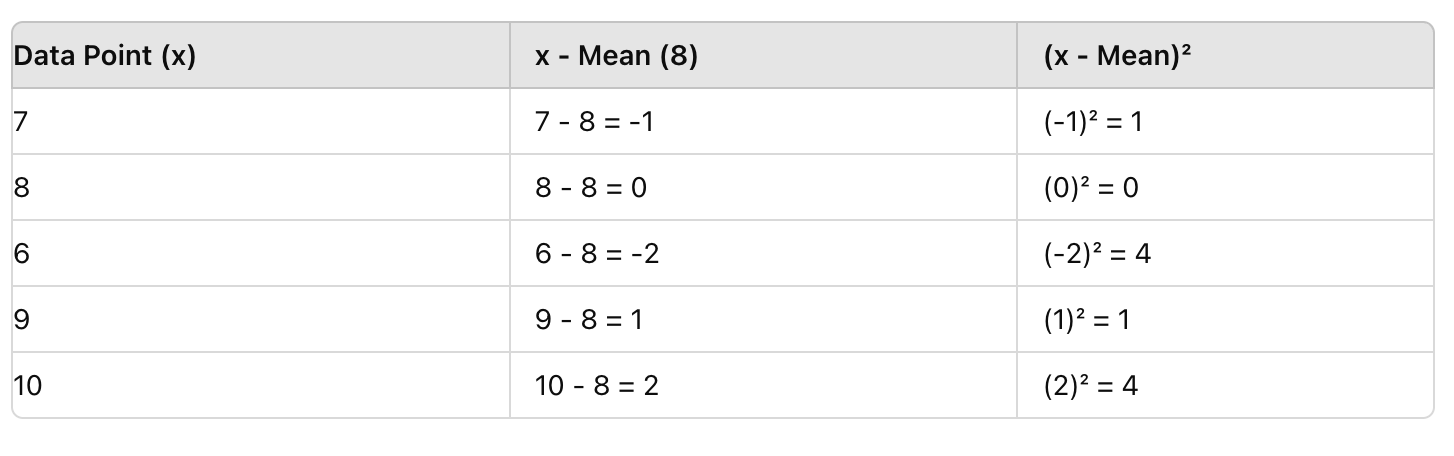Passo 3: Encontrar a Média das Diferenças ao Quadrado Agora, some as diferenças ao quadrado e divida pelo número de pontos de dados para calcular a variância. 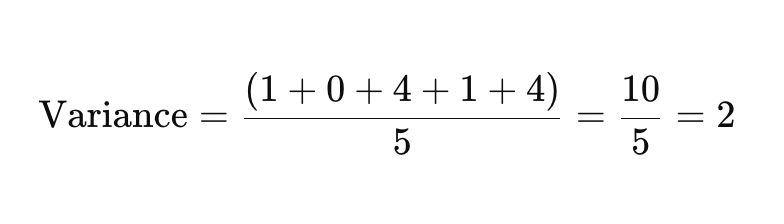Passo 4: Tirar a Raiz Quadrada da Variância Por fim, tire a raiz quadrada da variância para encontrar o desvio padrão. Neste exemplo, o desvio padrão é de aproximadamente 1.41. Isso significa que a maioria das pontuações de satisfação do cliente está dentro de 1.41 pontos da média (8). Como o desvio padrão é relativamente pequeno, as classificações estão bastante próximas da média, indicando consistência no feedback. Se o desvio padrão fosse maior, digamos 3 ou 4, sugeriria uma maior dispersão das respostas, com alguns clientes muito mais ou menos satisfeitos que outros. Desvio Padrão no Excel Guia Passo a Passo para Usar o Excel para o Desvio Padrão O Microsoft Excel ou o Google Sheets são ferramentas convenientes para calcular o desvio padrão. Veja como fazer: Insira seus dados em uma coluna. Selecione uma célula vazia onde deseja o resultado. Use a fórmula =STDEV.P() para o desvio padrão populacional ou =STDEV.S() para o desvio padrão amostral. Destacar seus dados, pressione Enter e o Excel calculará instantaneamente o resultado. O Excel automatiza o processo, economizando tempo e reduzindo a possibilidade de erros manuais. Exportando Dados do LimeSurvey para o Excel Com o LimeSurvey, você pode exportar seus dados de pesquisa diretamente para o Excel para analisar seus resultados. Para fazer isso: Navegue até a seção de resultados no LimeSurvey. Selecione a opção de exportação e escolha Excel como formato. Uma vez exportado, utilize as funções estatísticas do Excel, incluindo o desvio padrão, para obter uma compreensão mais profunda dos seus dados. Combinando as capacidades de coleta de dados do LimeSurvey com as ferramentas de análise do Excel, você pode interpretar e agir de forma eficiente sobre os resultados da sua pesquisa. Entendendo o Desvio Padrão Desvio Padrão vs. Erro Padrão O desvio padrão e o erro padrão estão relacionados, mas servem a propósitos diferentes. O desvio padrão mede a dispersão dos pontos de dados individuais, enquanto o erro padrão mede a precisão da média amostral em comparação com a média populacional real. Em pesquisas, o desvio padrão ajuda a entender a variabilidade nas respostas, enquanto o erro padrão é útil para estimar quão próxima é a média amostral da média populacional real. Desvio Padrão vs. Variância A variância é outra medida de dispersão de dados e é o quadrado do desvio padrão. Enquanto a variância ajuda a quantificar a magnitude da variabilidade, o desvio padrão é mais fácil de interpretar porque é expresso nas mesmas unidades que seus dados originais. Por exemplo, se você está medindo pontuações de satisfação, o desvio padrão fornecerá uma compreensão intuitiva de quão diferentes são as respostas em relação à média. Interpretando os Resultados do Desvio Padrão Uma vez que você tenha calculado o desvio padrão, pode usá-lo para interpretar a consistência das respostas da sua pesquisa. Um baixo desvio padrão significa que os respondentes geralmente estão de acordo, enquanto um alto desvio padrão sinaliza opiniões variadas. Por exemplo, imagine que você pesquisou 100 funcionários sobre sua satisfação no trabalho em uma escala de 1 a 10. Se a maioria das respostas estiver agrupada em torno de 8, com um pequeno desvio padrão, isso sugere satisfação geral. No entanto, se as classificações variam de 4 a 10, o desvio padrão maior mostra que as opiniões estão mais divididas, e você pode precisar investigar mais. Aplicações Práticas do Desvio Padrão Melhorando Perguntas da Pesquisa: Se você notar um grande desvio padrão para uma pergunta específica da pesquisa, pode indicar que a pergunta é ambígua ou não é bem compreendida pelos respondentes. Refinar a redação pode ajudar a coletar dados mais precisos em pesquisas futuras. Tomando Decisões Baseadas em Dados: O desvio padrão ajuda você a tomar decisões mais informadas ao revelar padrões nos dados da sua pesquisa. Por exemplo, se o feedback for altamente variável, você pode segmentar seu público e adaptar as respostas de acordo. Garantindo Precisão no Desvio Padrão Dados Faltantes: Dados faltantes podem distorcer seu cálculo de desvio padrão. Para evitar imprecisões, considere as respostas incompletas ou use técnicas de imputação. Evitar Outliers: Verificar seus dados em busca de erros ou outliers é essencial. Mesmo uma entrada incorreta pode alterar significativamente seus resultados. Usar as ferramentas de pesquisa do LimeSurvey pode ajudar você a coletar dados precisos e utilizáveis que refletam a verdadeira variabilidade. Ao começar com uma compreensão do desvio padrão, você desbloqueará insights poderosos sobre seus resultados de pesquisa. Isso permite que você interprete os dados de forma mais efetiva e tome melhores decisões com base em uma compreensão mais profunda de como seus respondentes se sentem, agem ou pensam. Após determinar o desvio padrão, o LimeSurvey permite que você melhore suas perguntas, para que você possa aproveitar ao máximo sua pesquisa e dados. Experimente hoje mesmo!