Tabelleninhalt
Stell dir vor, du führst eine Kundenzufriedenheitsumfrage für eine beliebte Café-Kette durch. Du erwartest, dass die meisten Kunden den Kaffee hoch bewerten – schließlich legt dein Café großen Wert auf Qualitätskontrolle und exzellenten Service. Doch die Ergebnisse sind durchmischt. Einige Kunden geben begeisterte Bewertungen, während andere anscheinend schlechte Erfahrungen gemacht haben. Was ist da los?
Hier kommt die Standardabweichung ins Spiel, um deine Daten zu quantifizieren, sodass du verstehst, ob die erhaltenen Antworten eng beieinander liegen oder stark variieren. Mit dieser Methode kannst du herausfinden, ob die wenigen niedrigen Bewertungen Ausreißer sind oder ob die Angebote deiner Marke tatsächlich inkonsistent sind.
Was ist die Standardabweichung?
Die Standardabweichung misst, wie stark die Werte in einem Datensatz streuen. Sie zeigt, wie weit einzelne Antworten vom Durchschnitt abweichen und hilft dir zu verstehen, ob deine Daten konsistent sind oder eine signifikante Varianz aufweisen. In der Umfragenanalyse liefert die Standardabweichung tiefere Einblicke in die Antworten der Menschen und ist ein wertvolles Werkzeug zur Interpretation der Ergebnisse.
Wenn alle Kunden beispielsweise deinen Service mit 8 oder 9 von 10 bewerten, wäre die Standardabweichung gering, was auf recht konsistente Ergebnisse hindeutet. Wenn einige jedoch mit 2 und andere mit 10 bewerten, wird die Standardabweichung viel größer sein, was auf unterschiedliche Meinungen hinweist.
Das Symbol für die Standardabweichung ist "σ" (kleines Sigma) für die Standardabweichung der Grundgesamtheit und "sss" für die Standardabweichung der Stichprobe. Es ist eine Abkürzung, die in statistischen Gleichungen und Formeln verwendet wird, um Varianz zu kennzeichnen.
Die Bedeutung der Standardabweichung in Umfragen
Die Standardabweichung bietet ein Maß für die Zuverlässigkeit der Antworten. Während die Durchschnittsbewertung eine schnelle Zusammenfassung geben kann, fügt die Standardabweichung Kontext hinzu. Sie zeigt, ob die meisten Antworten um diesen Durchschnitt gruppiert sind oder ob sie über einen breiten Bereich verteilt sind. Eine kleine Standardabweichung deutet auf Konsistenz hin, während eine große auf Variabilität hindeutet – was Unterschiede in der Interpretation oder Erfahrungen anzeigen kann.
Diese Messung ermöglicht es Forschern und Unternehmen, über die Oberfläche der Umfragedaten hinauszusehen, hilft ihnen, Bereiche zu identifizieren, in denen Meinungen divergieren, und leitet letztlich gezielte Verbesserungen oder Änderungen an.
Die Standardabweichung Schritt für Schritt berechnen, mit einem Beispiel
Die Berechnung der Standardabweichung mag zunächst komplex erscheinen, ist jedoch ein schrittweiser Prozess, der mit Übung einfacher wird. Berechne zuerst den Durchschnitt deiner Datensätze. Ziehe dann den Durchschnitt von jedem Datenpunkt ab, quadriere das Ergebnis und finde den Durchschnitt dieser quadrierten Abweichungen. Schließlich ziehe die Quadratwurzel von diesem Durchschnitt, um die Standardabweichung zu erhalten.
Beginnen wir mit folgender Formel:
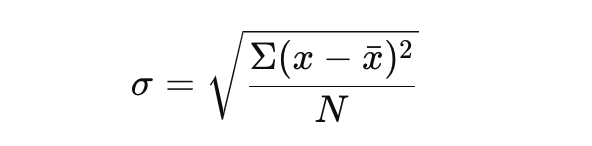
Diese Formel gibt dir ein klares Bild von der Variabilität in deinem Datensatz.
Angenommen, du hast eine Umfrage durchgeführt, in der 5 Kunden gebeten wurden, ihre Zufriedenheit mit deinem Service auf einer Skala von 1 bis 10 zu bewerten. Die Antworten waren: 7, 8, 6, 9, 10.
Nun berechnen wir die Standardabweichung für diesen Datensatz:
Schritt 1: Den Durchschnitt (Mittelwert) finden
Um den Durchschnitt zu finden, addiere alle Datenpunkte und teile durch die Anzahl der Antworten.
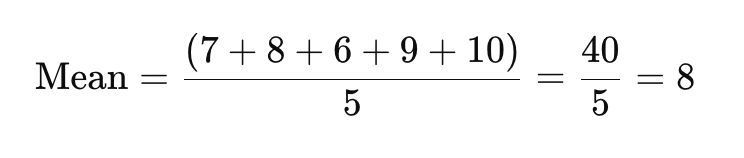
Der Durchschnittswert hier ist 8.
Schritt 2: Den Durchschnitt von jedem Datenpunkt abziehen und das Ergebnis quadrieren
Jetzt ziehe für jede Bewertung den Durchschnitt (8) ab und quadriere das Ergebnis. Dies entfernt negative Werte und hebt Abweichungen hervor.
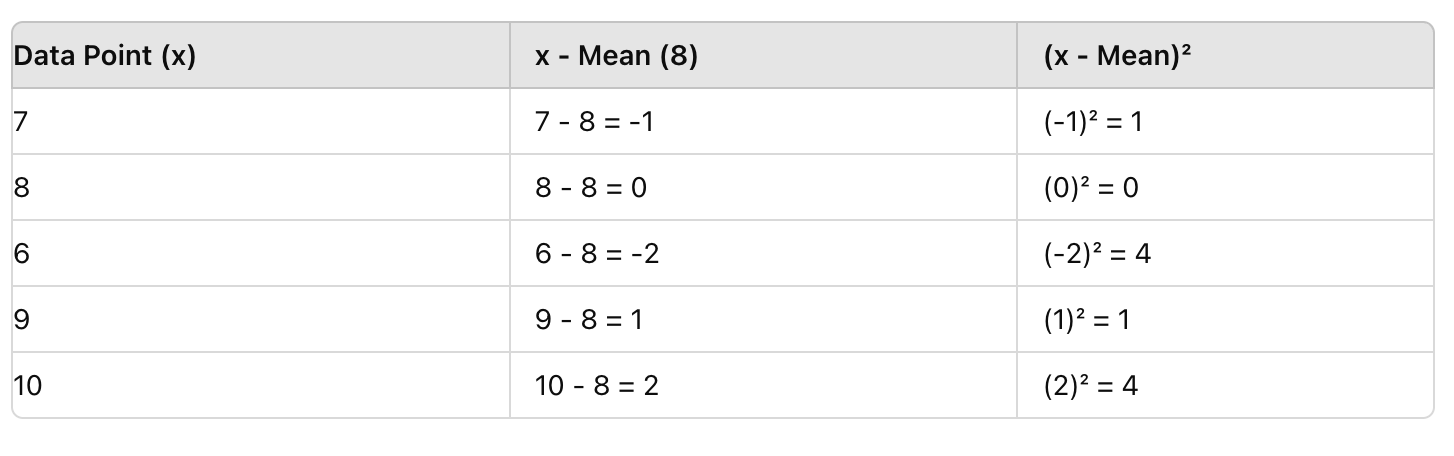
Schritt 3: Den Durchschnitt der quadrierten Abweichungen finden
Nun addiere die quadrierten Abweichungen und teile durch die Anzahl der Datenpunkte, um die Varianz zu finden.
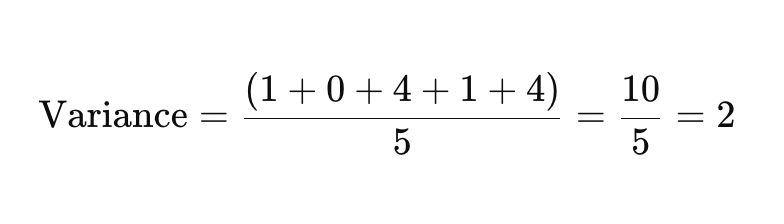
Schritt 4: Die Quadratwurzel der Varianz ziehen
Schließlich ziehe die Quadratwurzel der Varianz, um die Standardabweichung zu finden.

In diesem Beispiel beträgt die Standardabweichung ungefähr 1,41. Das bedeutet, dass die meisten Kundenzufriedenheitswerte innerhalb von 1,41 Punkten vom Durchschnittswert (8) liegen. Da die Standardabweichung relativ klein ist, sind die Bewertungen recht nahe am Durchschnitt, was auf Konsistenz im Feedback hinweist.
Wäre die Standardabweichung größer, zum Beispiel 3 oder 4, würde das eine breitere Streuung der Antworten nahelegen, wobei einige Kunden viel zufriedener oder unzufriedener als andere sind.
Standardabweichung in Excel
Schritt-für-Schritt-Anleitung zur Nutzung von Excel für die Standardabweichung
Microsoft Excel oder Google Sheets sind eines der praktischsten Werkzeuge zur Berechnung der Standardabweichung. So geht's:
- Gib deine Daten in eine Spalte ein.
- Wähle eine leere Zelle aus, in der du das Ergebnis haben möchtest.
- Verwende die Formel =STDEV.P() für die Standardabweichung der Grundgesamtheit oder =STDEV.S() für die Standardabweichung der Stichprobe.
- Markiere deine Daten, drücke Enter, und Excel berechnet sofort das Ergebnis.
Excel automatisiert den Prozess, spart Zeit und reduziert das Risiko manueller Fehler.
Exportieren von LimeSurvey-Daten nach Excel
Mit LimeSurvey kannst du deine Umfragedaten direkt nach Excel exportieren, um deine Ergebnisse weiter zu analysieren. Dazu:
- Navigiere zum Ergebnisbereich in LimeSurvey.
- Wähle die Exportoption und wähle Excel als Format aus.
- Nach dem Export benutze die statistischen Funktionen von Excel, einschließlich der Standardabweichung, um ein tieferes Verständnis deiner Daten zu erhalten.
Durch die Kombination der Datensammlung von LimeSurvey mit den Analysetools von Excel kannst du deine Umfrageergebnisse effizient interpretieren und darauf reagieren.
Standardabweichung verstehen
- Standardabweichung vs. Standardfehler
Standardabweichung und Standardfehler hängen zusammen, erfüllen jedoch unterschiedliche Zwecke. Die Standardabweichung misst die Streuung individueller Datenpunkte, während der Standardfehler die Genauigkeit des Stichprobenmittelwerts im Vergleich zum wahren Mittelwert der Population bewertet. Bei Umfragen hilft die Standardabweichung, die Variabilität der Antworten zu verstehen, während der Standardfehler nützlich ist, um abzuschätzen, wie nah dein Stichprobenmittelwert an dem tatsächlichen Mittelwert der Bevölkerung ist. - Standardabweichung vs. Varianz
Varianz ist ein weiteres Maß für die Streuung von Daten und das Quadrat der Standardabweichung. Während die Varianz hilft, das Ausmaß der Variabilität zu quantifizieren, ist die Standardabweichung leichter zu interpretieren, da sie in denselben Einheiten wie deine ursprünglichen Daten ausgedrückt wird. Wenn du beispielsweise Zufriedenheitswerte misst, bietet die Standardabweichung ein intuitives Verständnis davon, wie sehr die Antworten vom Durchschnitt abweichen.
Interpretation der Ergebnisse der Standardabweichung
Sobald du die Standardabweichung berechnet hast, kannst du sie nutzen, um die Konsistenz deiner Umfrageantworten zu interpretieren. Eine niedrige Standardabweichung bedeutet, dass die Befragten im Allgemeinen übereinstimmen, während eine hohe Standardabweichung auf unterschiedliche Meinungen hindeutet.
Wenn du beispielsweise 100 Mitarbeiter zu ihrer Arbeitszufriedenheit auf einer Skala von 1 bis 10 befragt hast und die meisten Antworten um 8 gruppiert sind, mit einer kleinen Standardabweichung, deutet dies auf allgemeine Zufriedenheit hin. Wenn die Bewertungen jedoch von 4 bis 10 reichen, zeigt die größere Standardabweichung, dass die Meinungen stärker geteilt sind, und du möglicherweise weiter untersuchen musst.
Praktische Anwendungen der Standardabweichung
- Verbesserung von Umfragefragen: Wenn du eine große Standardabweichung für eine spezifische Umfragefrage feststellst, könnte dies darauf hindeuten, dass die Frage mehrdeutig ist oder von den Befragten nicht gut verstanden wird. Eine Verfeinerung der Formulierung kann helfen, in zukünftigen Umfragen genauere Daten zu sammeln.
- Datenbasierte Entscheidungen treffen: Die Standardabweichung hilft dir, fundiertere Entscheidungen zu treffen, indem sie Muster in deinen Umfragedaten aufdeckt. Wenn das Feedback hochvariabel ist, kannst du dein Publikum segmentieren und entsprechend maßgeschneiderte Antworten geben.
Genauigkeit bei der Standardabweichung sicherstellen
- Fehlende Daten: Fehlende Daten können deine Berechnung der Standardabweichung verzerren. Um Ungenauigkeiten zu vermeiden, solltest du entweder fehlende Daten berücksichtigen, indem du unvollständige Antworten ausschließt, oder Imputationstechniken verwenden.
- Ausreißer vermeiden: Es ist wichtig, deine Daten auf Fehler oder Ausreißer zu überprüfen. Selbst ein falscher Eintrag kann deine Ergebnisse erheblich verändern. Die Verwendung der Umfragetools von LimeSurvey kann dir helfen, genaue, verwertbare Daten zu sammeln, die die wahre Variabilität widerspiegeln.
Durch das Verständnis der Standardabweichung erhältst du wertvolle Einblicke in deine Umfrageergebnisse. Dies ermöglicht dir nicht nur eine effektivere Interpretation der Daten, sondern auch bessere Entscheidungen auf der Grundlage eines tieferen Verständnisses dafür, wie sich deine Befragten fühlen, handeln oder denken.
Nachdem du die Standardabweichung bestimmt hast, ermöglicht dir LimeSurvey, deine Fragen zu verbessern, sodass du das Beste aus deiner Umfrage und deinen Daten herausholen kannst.




