Середнє квадратичне відхилення: Все, що вам потрібно знати для опитувань.

Уявіть, що ви проводите опитування задоволеності клієнтів для популярної мережі кафе. Ви очікуєте, що більшість клієнтів високо оцінить каву — зрештою, ваше кафе пишається контролем якості та відмінним обслуговуванням. Але, переглянувши результати, ви виявляєте, що оцінки відрізняються: деякі клієнти залишили позитивні відгуки, а інші, здається, мали поганий досвід. Що трапилось? Тут стандартне відхилення допомагає кількісно визначити ваші дані, дозволяючи зрозуміти, чи відповіді близькі одна до одної чи сильно варіюються. Цей метод допоможе виявити, чи є кілька низьких оцінок винятками, або ж пропозиції вашого бренду дійсно не послідовні. Що таке стандартне відхилення? Стандартне відхилення в основному вимірює, як розподілені значення в наборі даних. Воно показує, наскільки індивідуальні відповіді відхиляються від середнього, допомагаючи зрозуміти, чи є ваші дані послідовними, чи містять значну варіативність. У аналізі опитувань стандартне відхилення надає глибші уявлення про відповіді людей, що робить його цінним інструментом для інтерпретації результатів. Наприклад, якщо всі ваші клієнти оцінюють ваше обслуговування на 8 або 9 з 10, у вас буде маленьке стандартне відхилення, що означає, що результати досить послідовні. З іншого боку, якщо деякі оцінюють на 2, а інші на 10, стандартне відхилення буде значно більшим, що сигналізує про різноманітність думок. Символом стандартного відхилення є “σ” (маленька сигма) для стандартного відхилення популяції та “sss” для стандартного відхилення вибірки. Це скорочення, яке використовується в статистичних рівняннях та формулах для позначення варіативності. Важливість стандартного відхилення в опитуваннях Стандартне відхилення забезпечує вимір надійності відповідей. Хоча середня оцінка може надати швидке резюме, стандартне відхилення додає контекст. Воно показує, чи більшість відповідей зосереджені навколо цього середнього чи розподілені по широкому діапазону. Маленьке стандартне відхилення вказує на послідовність, а велике — на варіативність, що може вказувати на різницю в інтерпретації чи досвіді. Ця вимірка дозволяє дослідникам і бізнесу бачити глибше дані про опитування, допомагаючи виявити області, де думки розходяться, а в кінцевому результаті — спрямовувати більш цілеспрямовані покращення чи зміни. Покроковий розрахунок стандартного відхилення з прикладом Розрахунок стандартного відхилення може спочатку здаватися складним, але це покроковий процес, який стає простішим з практикою. Спочатку розрахуйте середнє (середнє арифметичне) вашого набору даних. Потім відніміть середнє від кожної точки даних, піднесіть результат до квадрату, і знайдіть середнє цих квадратованих відхилень. Нарешті, витягніть квадратний корінь з цього середнього, щоб отримати стандартне відхилення. 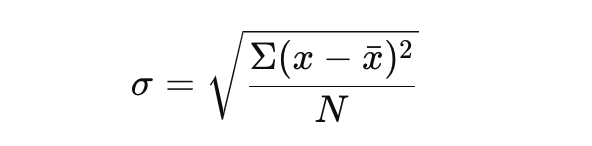Розглянемо наступну формулу: Ця формула надає чітке уявлення про варіативність у вашому наборі даних. Припустимо, ви провели опитування, попросивши 5 клієнтів оцінити своє задоволення вашим обслуговуванням за шкалою від 1 до 10. Відповіді були: 7, 8, 6, 9, 10. Тепер розрахуємо стандартне відхилення для цього набору даних: Крок 1: Знайдіть середнє (середнє арифметичне) Щоб знайти середнє, додайте всі дані разом і поділіть на кількість відповідей. 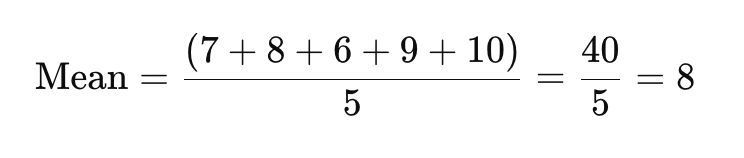Середня оцінка задоволеності тут дорівнює 8. Крок 2: Відніміть середнє від кожної точки даних і піднесіть результат до квадрату Далі для кожної оцінки відніміть середнє (8), потім піднесіть результат до квадрату. Це усуває негативні значення та підкреслює відхилення. 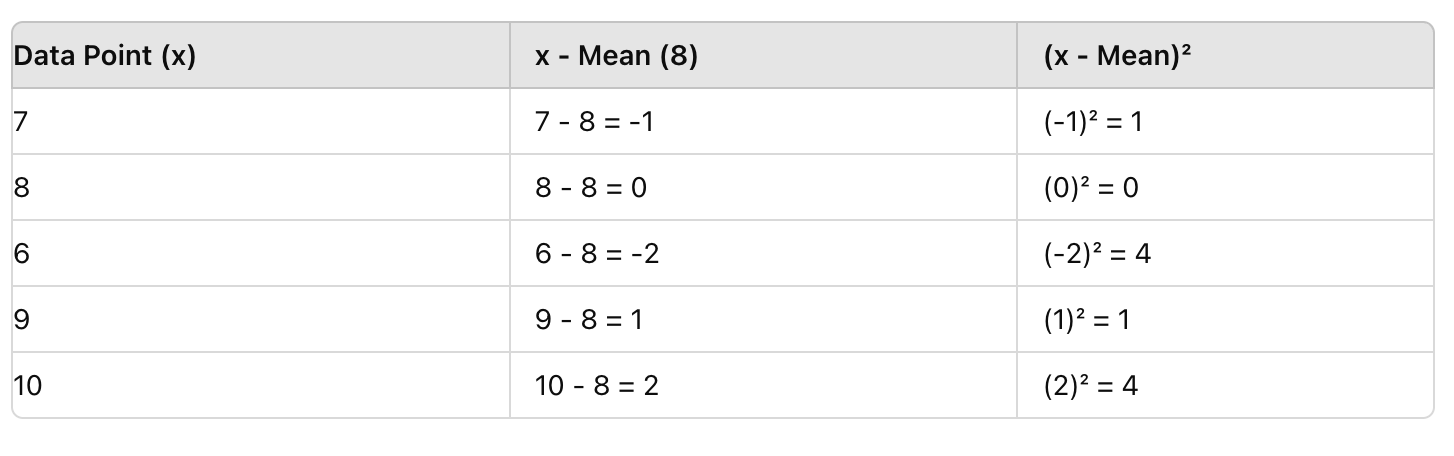Крок 3: Знайдіть середнє квадратних відхилень Тепер складіть квадратні відхилення і розділіть на кількість точок даних, щоб знайти дисперсію. 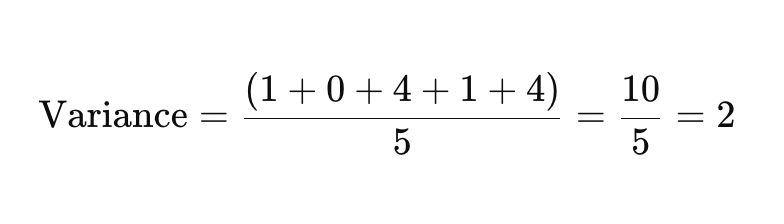Крок 4: Витягніть квадратний корінь з дисперсії Нарешті, витягніть квадратний корінь з дисперсії, щоб знайти стандартне відхилення. У цьому прикладі стандартне відхилення приблизно дорівнює 1.41. Це означає, що більшість оцінок задоволеності клієнтів знаходяться в межах 1.41 пункту від середньої оцінки (8). Оскільки стандартне відхилення відносно мале, оцінки досить близькі до середнього, що вказує на послідовність відгуків. Якщо б стандартне відхилення було більшим, скажімо, 3 або 4, це б свідчило про ширше розподілення відповідей, де деякі клієнти значно більше чи менше задоволені, ніж інші. Стандартне відхилення в Excel Покрокова інструкція щодо використання Excel для стандартного відхилення Microsoft Excel або Google Sheets є одним із найзручніших інструментів для розрахунку стандартного відхилення. Ось як це зробити: Введіть ваші дані в стовпчик. Виберіть порожню клітинку, де хочете отримати результат. Використовуйте формулу =STDEV.P() для стандартного відхилення популяції або =STDEV.S() для стандартного відхилення вибірки. Виділіть ваші дані, натисніть Enter, і Excel миттєво розрахує результат. Excel автоматизує процес, економлячи ваш час і зменшуючи ймовірність помилок. Експорт даних LimeSurvey до Excel У LimeSurvey ви можете експортувати дані вашого опитування безпосередньо в Excel для подальшого аналізу результатів. Для цього: Перейдіть до розділу результатів в LimeSurvey. Виберіть опцію експорту та виберіть Excel як формат. Після експорту використовуйте статистичні функції Excel, включаючи стандартне відхилення, щоб краще зрозуміти ваші дані. Поєднуючи можливості збору даних LimeSurvey з аналітичними інструментами Excel, ви зможете ефективно інтерпретувати та діяти на результати опитування. Розуміння стандартного відхилення Стандартне відхилення проти стандартної помилки Стандартне відхилення та стандартна помилка пов'язані, але слугують різним цілям. Стандартне відхилення вимірює розподіл окремих точок даних, в той час як стандартна помилка вимірює точність середнього вибірки відносно справжнього середнього в популяції. У опитуваннях стандартне відхилення допомагає зрозуміти варіативність відповідей, тоді як стандартна помилка корисна для оцінки того, наскільки близьке ваше середнє зразка до реального середнього в популяції. Стандартне відхилення проти дисперсії Дисперсія є ще одним виміром розподілу даних і є квадратом стандартного відхилення. Хоча дисперсія допомагає кількісно визначити величину варіативності, стандартне відхилення легше інтерпретувати, оскільки воно виражається в тих самих одиницях, що і ваші вихідні дані. Наприклад, якщо ви вимірюєте оцінки задоволеності, стандартне відхилення надасть інтуїтивне розуміння того, наскільки відповіді відрізняються від середнього. Інтерпретація результатів стандартного відхилення Після того, як ви розрахували стандартне відхилення, ви можете використовувати його для інтерпретації послідовності ваших відповідей на опитування. Низьке стандартне відхилення означає, що респонденти загалом згодні, тоді як високе стандартне відхилення сигналізує про різні думки. Наприклад, уявімо, що ви опитали 100 працівників щодо їх задоволеності роботою за шкалою від 1 до 10. Якщо більшість відповідей зосереджені навколо 8, з малим стандартним відхиленням, це свідчить про загальне задоволення. Однак, якщо оцінки варіюються від 4 до 10, велике стандартне відхилення показує, що думки більш поділені, і вам, можливо, потрібно дослідити це далі. Практичні застосування стандартного відхилення Покращення запитань в опитуваннях: Якщо ви помітили велике стандартне відхилення для конкретного питання опитування, це може свідчити про те, що питання є неоднозначним або не зовсім зрозумілим для респондентів. Поліпшивши формулювання, ви зможете зібрати більш точні дані в майбутніх опитуваннях. Прийняття рішень на основі даних: Стандартне відхилення допомагає вам приймати більш обґрунтовані рішення, виявляючи закономірності у ваших даних опитування. Наприклад, якщо відгуки дуже різноманітні, ви можете сегментувати свою аудиторію та адаптувати відповіді відповідно. Забезпечення точності в стандартному відхиленні Відсутні дані: Відсутні дані можуть спотворити ваш розрахунок стандартного відхилення. Щоб уникнути неточностей, або врахуйте відсутні дані, виключивши неповні відповіді, або використовуйте методи імпутації. Уникнення викидів: Подвійна перевірка ваших даних на помилки чи викиди є необхідною. Навіть один неправильний запис може значно змінити ваші результати. Використання інструментів опитування LimeSurvey може допомогти вам зібрати точні, використані дані, що відображають справжню варіативність. Ознайомившись зі стандартним відхиленням, ви отримаєте потужні уявлення про результати вашого опитування. Це дозволить вам не лише ефективно інтерпретувати дані, але й приймати кращі рішення на основі глибшого розуміння того, як почуваються, діють або мислять ваші респонденти. Після визначення стандартного відхилення LimeSurvey дозволяє вам покращувати ваші питання, щоб ви могли максимально ефективно використати ваше опитування та дані. Спробуйте сьогодні!