Směrodatná odchylka: vše, co potřebujete vědět pro průzkumy.

Představte si, že provádíte anketu o spokojenosti zákazníků pro populární řetězec kaváren. Očekáváte, že většina zákazníků ocení kávu vysoko – koneckonců, vaše kavárna si zakládá na kvalitě a skvělé službě. Když se však podíváte na výsledky, hodnocení jsou velmi rozmanitá. Někteří zákazníci vám dávají skvělé recenze, zatímco jiní mají špatnou zkušenost. Co se děje? V této situaci vám standardní odchylka pomůže kvantifikovat vaše data, což vám umožní pochopit, zda jsou odpovědi blízko sebe nebo se naopak značně liší. Tímto způsobem můžete zjistit, zda jsou nízké hodnocení výjimky, nebo jestli jsou nabídky vaší značky opravdu nekonzistentní. Co je to standardní odchylka? Standardní odchylka v jádru měří, jak moc jsou hodnoty v datovém souboru rozptýlené. Říká vám, jak moc se jednotlivé odpovědi odchylují od průměru, což vám pomůže pochopit, zda jsou vaše data konzistentní, nebo zda vykazují významnou variabilitu. V analýze průzkumů dává standardní odchylka hlubší náhled na to, jak lidé reagují, což z ní činí cenný nástroj pro interpretaci výsledků. Například, pokud všichni vaši zákazníci hodnotí vaše služby 8 nebo 9 z 10, budete mít malou standardní odchylku, což znamená, že výsledky jsou docela konzistentní. Na druhou stranu, pokud někteří hodnotí 2 a jiní 10, standardní odchylka bude mnohem větší, což signalizuje rozmanité názory. Symbol pro standardní odchylku je „σ“ (malé sigma) pro populaci a „sss“ pro vzorek. To je zkratka používaná ve statistických rovnicích a vzorcích k označení variability. Důležitost standardní odchylky v průzkumech Standardní odchylka poskytuje míru spolehlivosti v odpovědích. Zatímco průměrné (nebo aritmetické) skóre vám může poskytnout rychlý přehled, standardní odchylka přidává kontext. Ukazuje, zda jsou většina odpovědí soustředěna kolem tohoto průměru, nebo zda jsou rozložena v širokém rozpětí. Malá standardní odchylka naznačuje konzistenci, zatímco velká naznačuje variabilitu – což může naznačovat rozdíly v interpretaci nebo zkušenosti. Toto měření umožňuje výzkumníkům a firmám nahlédnout za povrch dat průzkumu, přičemž jim pomáhá identifikovat oblasti, kde se názory rozcházejí, a konečně řídit cílenější zlepšení nebo změny. Výpočet standardní odchylky krok za krokem, na příkladu Výpočet standardní odchylky se na první pohled může zdát složitý, ale je to krok za krokem proces, který se s praxí stává snadnějším. Nejprve vypočítejte průměr (aritmetický) vaší datové sady. Poté od každého bodu dat odečtěte průměr, na druhou umocněte výsledek a najděte průměr těchto umocněných rozdílů. Nakonec vezměte druhou odmocninu tohoto průměru, abyste získali standardní odchylku. 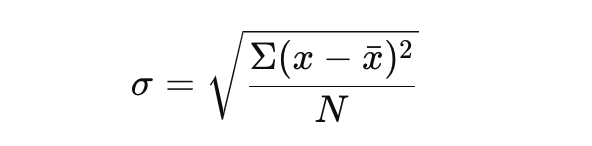Začněme použitím následujícího vzorce: Tento vzorec vám dává jasný obraz o variabilitě vaší datové sady. Řekněme, že jste provedli průzkum, ve kterém jste požádali 5 zákazníků, aby ohodnotili svou spokojenost s vašimi službami na škále od 1 do 10. Odpovědi byly: 7, 8, 6, 9, 10. Teď si spočítáme standardní odchylku pro tento datový soubor: Krok 1: Najděte průměr (aritmetický) Abyste nalezli průměr, sečtěte všechny body dat a vydělte je počtem odpovědí. 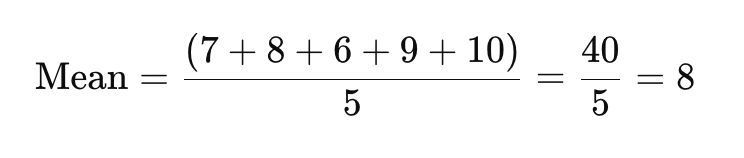Průměrné skóre spokojenosti je zde 8. Krok 2: Odečtěte průměr od každého bodu dat a umocněte výsledek Dále, pro každé skóre odečtěte průměr (8), a potom umocněte výsledek. To odstraňuje záporné hodnoty a zvýrazňuje odchylky. 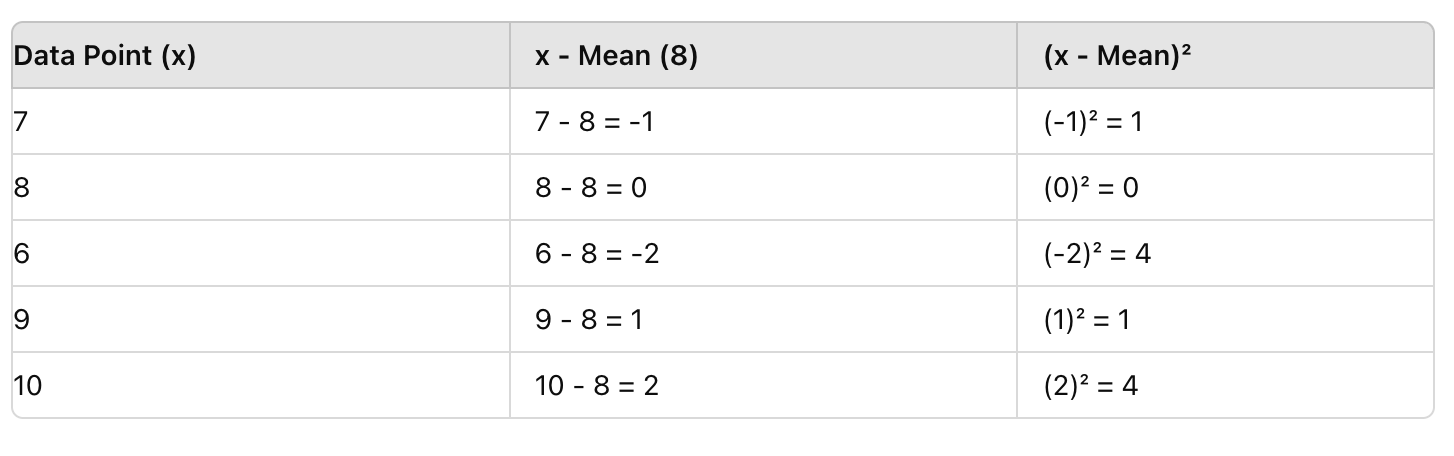Krok 3: Najděte průměr umocněných rozdílů Nyní sečtěte umocněné rozdíly a vydělte je počtem bodů dat, abyste našli rozptyl. 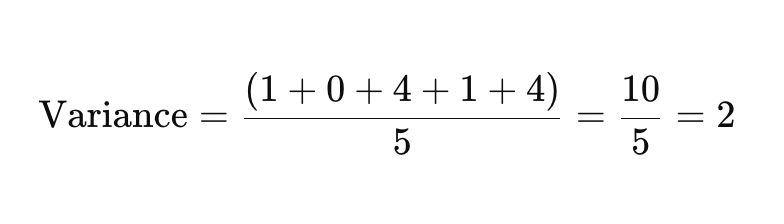Krok 4: Vezměte druhou odmocninu rozptylu Nakonec vezměte druhou odmocninu rozptylu, abyste našli standardní odchylku. V tomto příkladu je standardní odchylka přibližně 1.41. To znamená, že většina skóre spokojenosti zákazníků je v rozmezí 1.41 bodů od průměrného skóre (8). Protože je standardní odchylka relativně malá, hodnocení jsou docela blízko průměru, což naznačuje konzistenci v hodnocení. Pokud by byla standardní odchylka větší, například 3 nebo 4, naznačovalo by to širší rozšíření odpovědí, přičemž někteří zákazníci by byli mnohem spokojenější nebo nespokojení než ostatní. Standardní odchylka v Excelu Krok za krokem, jak používat Excel pro standardní odchylku Microsoft Excel nebo Google Sheets je jedno z nejpohodlnějších nástrojů pro výpočet standardní odchylky. Zde je návod, jak to udělat: Zadejte svá data do sloupce. Vyberte prázdnou buňku, kde chcete výsledek. Použijte vzorec =STDEV.P() pro standardní odchylku populace nebo =STDEV.S() pro standardní odchylku vzorku. Vyberte svá data, stiskněte Enter a Excel okamžitě vypočítá výsledek. Excel automatizuje proces, což vám šetří čas a snižuje riziko ručních chyb. Export dat z LimeSurvey do Excelu S LimeSurvey můžete exportovat svá data z průzkumu přímo do Excelu pro další analýzu vašich výsledků. K tomu: Přejděte do sekce výsledků v LimeSurvey. Vyberte možnost exportu a zvolte Excel jako formát. Jakmile je exportováno, použijte Excel k analýze včetně funkcí standardní odchylky pro hlubší pochopení vašich dat. Spojením sachamuků sběru dat od LimeSurvey s analytickými nástroji Excelu můžete efektivně interpretovat a reagovat na výsledky vašeho průzkumu. Pochopení standardní odchylky Standardní odchylka vs. standardní chyba Standardní odchylka a standardní chyba jsou si příbuzné, ale slouží různým účelům. Standardní odchylka měří rozptyl jednotlivých datových bodů, zatímco standardní chyba měří přesnost vzorku ve vztahu k skutečnému průměru populace. V průzkumech standardní odchylka pomáhá pochopit variabilitu v odpovědích, zatímco standardní chyba je užitečná pro odhad, jak blízko je průměr vzorku skutečnému průměru populace. Standardní odchylka vs. rozptyl Rozptyl je další míra rozptylu dat a je to čtverec standardní odchylky. Zatímco rozptyl pomáhá kvantifikovat velikost variability, standardní odchylka je snazší pro interpretaci, protože je vyjádřena ve stejných jednotkách jako původní data. Například pokud měříte skóre spokojenosti, standardní odchylka poskytne intuitivní pochopení, jak moc se odpovědi liší od průměru. Interpretace výsledků standardní odchylky Až vypočítáte standardní odchylku, můžete ji použít k interpretaci konzistence vašich odpovědí v průzkumu. Nízká standardní odchylka znamená, že respondenti se většinou shodují, zatímco vysoká standardní odchylka signalizuje různorodost názorů. Příklad, představte si, že jste provedli průzkum mezi 100 zaměstnanci o jejich spokojenosti s prací na škále od 1 do 10. Pokud jsou většina odpovědí soustředěny kolem 8, s malou standardní odchylkou, naznačuje to obecnou spokojenost. Naopak, pokud se hodnocení pohybují od 4 do 10, vyšší standardní odchylka ukazuje na rozdělenější názory a možná budete muset dále zkoumat situaci. Praktické aplikace standardní odchylky Zlepšení otázek v průzkumech: Pokud si všimnete vysoké standardní odchylky u konkrétní otázky v průzkumu, může to naznačovat, že otázka je nejasná nebo není respondenty dobře pochopena. Vylepšení formulace může pomoci shromažďovat přesnější data v budoucích průzkumech. Rozhodování založené na datech: Standardní odchylka vám pomáhá činit informovanější rozhodnutí odhalením vzorců ve vašich datách z průzkumu. Například, pokud je zpětná vazba značně variabilní, můžete segmentovat svou cílovou skupinu a přizpůsobit příslušné reakce. Zajištění přesnosti standardní odchylky Chybějící data: Chybějící data mohou zkreslit výpočet standardní odchylky. Aby se předešlo nepřesnostem, buďto započítejte chybějící data tím, že vyloučíte neúplné odpovědi, nebo použijte imputace techniky. Vyhýbání se extrémním hodnotám: Důležité je dvakrát zkontrolovat svá data na chyby nebo extrémní hodnoty. I jediný nesprávný záznam může významně změnit vaše výsledky. Použití nástrojů průzkumu LimeSurvey vám může pomoci shromáždit přesná, použitelná data, která odrážejí skutečnou variabilitu. Začleněním porozumění standardní odchylce odemknete mocné vhledy do vašich výsledků z průzkumu. To vám umožní nejen lépe interpretovat data, ale také přijímat lepší rozhodnutí na základě hlubšího pochopení toho, jak vaši respondenti cítí, jednají nebo myslí. Po určení standardní odchylky vám LimeSurvey umožňuje zlepšit vaše otázky, aby jste mohli co nejlépe využít svůj průzkum a data. Vyzkoušejte to dnes!