Deviazione standard: tutto ciò che devi sapere per i sondaggi

Immagina di condurre un sondaggio sulla soddisfazione dei clienti per una catena di caffè popolare. Ti aspetti che la maggior parte dei clienti valuti il caffè molto positivamente, dato che il tuo caffè si vanta di avere un controllo qualità e un servizio eccellente. Ma, analizzando i risultati, noti che le valutazioni sono molto variabili. Alcuni clienti lasciano recensioni entusiastiche, mentre altri sembrano aver avuto un’esperienza negativa. Cosa sta succedendo? Qui entra in gioco la deviazione standard, che aiuta a quantificare i dati, permettendoti di capire se le risposte ricevute sono allineate o se variano notevolmente. Con questo metodo, puoi scoprire se quei pochi punteggi bassi sono casi isolati o se le offerte del tuo marchio sono davvero inconsistenti. Che cos'è la Deviazione Standard? In sostanza, la deviazione standard misura quanto siano disperse le valori in un dataset. Indica quanto le risposte individuali si discostano dalla media, aiutandoti a capire se i tuoi dati sono coerenti o presentano una significativa variabilità. Nella analisi dei sondaggi, la deviazione standard fornisce approfondimenti più profondi su come le persone rispondono, rendendola uno strumento prezioso per interpretare i risultati. Ad esempio, se tutti i tuoi clienti valutano il tuo servizio con un 8 o 9 su 10, avresti una piccola deviazione standard, il che significa che i risultati sono abbastanza coerenti. D'altro canto, se alcuni danno un 2 e altri un 10, la deviazione standard sarà molto più alta, segnalando opinioni più diverse. Il simbolo per la deviazione standard è “σ” (sigma minuscola) per la deviazione standard della popolazione e “sss” per la deviazione standard del campione. È una forma abbreviata utilizzata nelle equazioni e formule statistiche per denotare variabilità. L'importanza della Deviazione Standard nei Sondaggi La deviazione standard fornisce una misura di affidabilità nelle risposte. Sebbene il punteggio medio possa darti un sommario rapido, la deviazione standard aggiunge contesto. Mostra se la maggior parte delle risposte sono raggruppate attorno a quella media o se sono distribuite su un ampio intervallo. Una piccola deviazione standard suggerisce coerenza, mentre una grande indica variabilità, che potrebbe segnalare differenze nell'interpretazione o nell'esperienza. Questa misura consente a ricercatori e imprese di andare oltre la superficie dei dati del sondaggio, aiutandoli a identificare aree in cui le opinioni divergono e, infine, guidando miglioramenti o cambiamenti mirati. Calcolare la Deviazione Standard Fase per Fase, con un Esempio Calcolare la deviazione standard potrebbe sembrare complesso all'inizio, ma è un processo passo-passo che diventa più semplice con la pratica. Prima, calcola la media (media) del tuo dataset. Poi, sottrai la media da ciascun punto dati, quadrati il risultato e trova la media di queste differenze quadrate. Infine, prendi la radice quadrata di questa media per ottenere la deviazione standard. 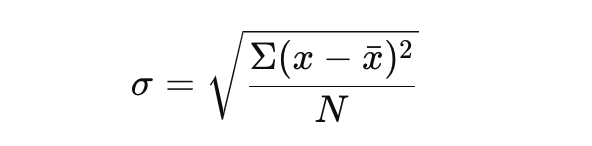Iniziamo utilizzando la seguente formula: Questa formula ti dà un’immagine chiara della variabilità nel tuo dataset. Diciamo che hai condotto un sondaggio chiedendo a 5 clienti di valutare la loro soddisfazione con il tuo servizio su una scala da 1 a 10. Le risposte sono state: 7, 8, 6, 9, 10. Ora, calcoliamo la deviazione standard per questo dataset: Passo 1: Trova la Media (Media) Per trovare la media, somma tutti i punti dati insieme e dividi per il numero di risposte. 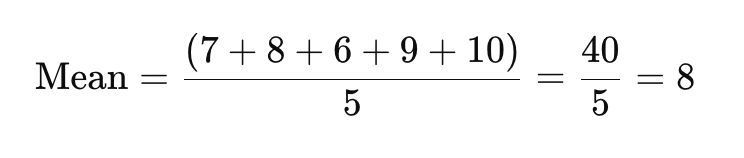Il punteggio medio di soddisfazione qui è 8. Passo 2: Sottrai la Media da Ogni Punto Dati e Quadrati il Risultato Successivamente, per ogni punteggio, sottrai la media (8), quindi quadrati il risultato. Questo rimuove i valori negativi ed evidenzia le deviazioni. 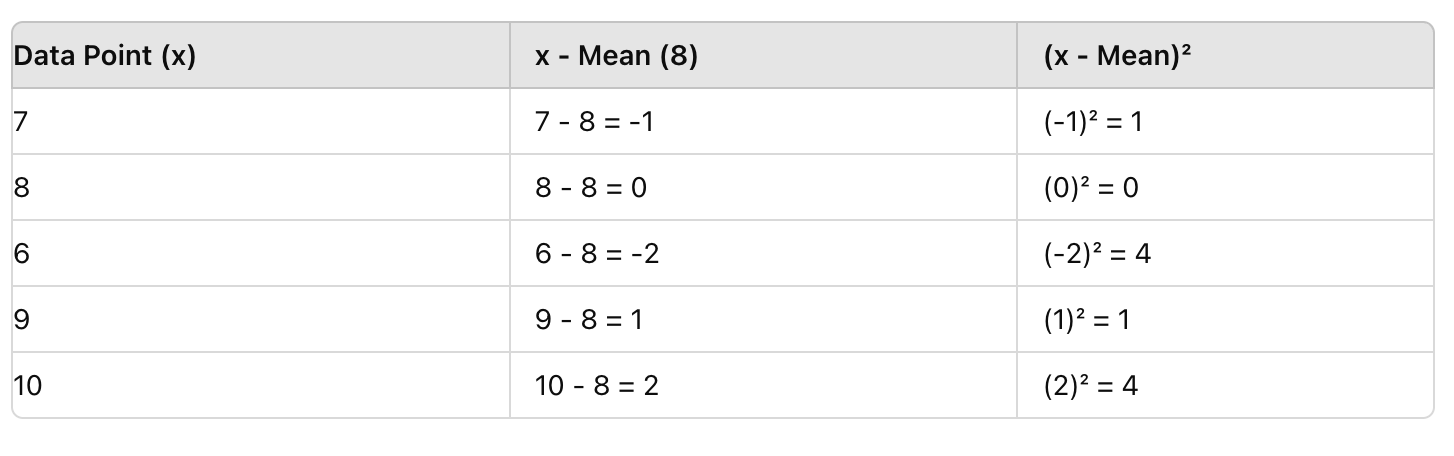Passo 3: Trova la Media delle Differenze Quadrate Ora, somma le differenze quadrate e dividi per il numero di punti dati per trovare la varianza. 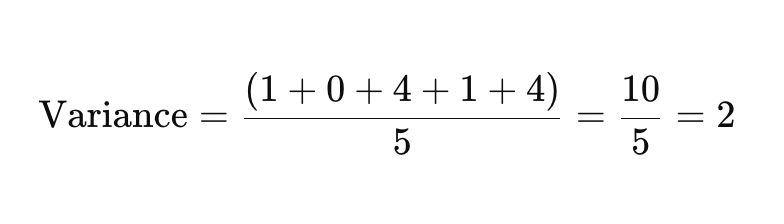Passo 4: Prendi la Radice Quadrata della Varianza Infine, prendi la radice quadrata della varianza per trovare la deviazione standard. In questo esempio, la deviazione standard è approssimativamente 1.41. Questo significa che la maggior parte dei punteggi di soddisfazione dei clienti è entro 1.41 punti dal punteggio medio (8). Poiché la deviazione standard è relativamente piccola, le valutazioni sono abbastanza vicine alla media, indicando coerenza nel feedback. Se la deviazione standard fosse più grande, ad esempio 3 o 4, suggerirebbe una diffusione più ampia delle risposte, con alcuni clienti molto più o meno soddisfatti di altri. Deviazione Standard in Excel Guida Passo-Passo per Utilizzare Excel per la Deviazione Standard Microsoft Excel o Google Sheets sono tra gli strumenti più comodi per calcolare la deviazione standard. Ecco come fare: Inserisci i tuoi dati in una colonna. Seleziona una cella vuota dove desideri il risultato. Usa la formula =STDEV.P() per la deviazione standard della popolazione o =STDEV.S() per la deviazione standard del campione. Seleziona i tuoi dati, premi Invio ed Excel calcolerà istantaneamente il risultato. Excel automatizza il processo, risparmiando tempo e riducendo potenziali errori manuali. Esportare Dati di LimeSurvey in Excel Con LimeSurvey, puoi esportare i dati del tuo sondaggio direttamente in Excel per analizzare ulteriormente i risultati. Per farlo: Vai alla sezione risultati in LimeSurvey. Seleziona l'opzione di esportazione e scegli Excel come formato. Una volta esportato, utilizza le funzioni statistiche di Excel, inclusa la deviazione standard, per ottenere una comprensione più profonda dei tuoi dati. Combinando le capacità di raccolta dati di LimeSurvey con gli strumenti di analisi di Excel, puoi interpretare e agire sui risultati del tuo sondaggio in modo efficiente. Comprendere la Deviazione Standard Deviazione Standard vs. Errore Standard La deviazione standard e l'errore standard sono correlati, ma servono a scopi diversi. La deviazione standard misura la diffusione dei singoli punti dati, mentre l'errore standard misura l'accuratezza della media del campione rispetto alla reale media della popolazione. Nei sondaggi, la deviazione standard aiuta a comprendere la variabilità nelle risposte, mentre l'errore standard è utile per stimare quanto sia vicina la tua media campionaria alla vera media della popolazione. Deviazione Standard vs. Varianza La varianza è un'altra misura della dispersione dei dati e rappresenta il quadrato della deviazione standard. Mentre la varianza aiuta a quantificare l'entità della variabilità, la deviazione standard è più facile da interpretare perché è espressa nelle stesse unità dei tuoi dati originali. Ad esempio, se stai misurando punteggi di soddisfazione, la deviazione standard fornirà una comprensione intuitiva di quanto le risposte differiscano dalla media. Interpretare i Risultati della Deviazione Standard Dopo aver calcolato la deviazione standard, puoi utilizzarla per interpretare la coerenza delle risposte del tuo sondaggio. Una bassa deviazione standard significa che i rispondenti sono generalmente d'accordo, mentre una alta deviazione standard segnala opinioni variegate. Ad esempio, immagina di aver sondato 100 dipendenti sulla loro soddisfazione lavorativa su una scala da 1 a 10. Se la maggior parte delle risposte è raggruppata attorno a 8, con una piccola deviazione standard, suggerisce soddisfazione generale. Tuttavia, se le valutazioni variano da 4 a 10, la maggiore deviazione standard mostra che le opinioni sono più divise, quindi potrebbe essere necessario indagare ulteriormente. Applicazioni Pratiche della Deviazione Standard Migliorare le Domande del Sondaggio: Se noti una grande deviazione standard per una specifica domanda del sondaggio, potrebbe indicare che la domanda è ambigua o non ben compresa dai rispondenti. Raffinare la formulazione può aiutare a raccogliere dati più accurati in futuri sondaggi. Prendere Decisioni Basate sui Dati: La deviazione standard ti aiuta a prendere decisioni più informate rivelando schemi nei tuoi dati di sondaggio. Ad esempio, se il feedback è altamente variabile, puoi segmentare il tuo pubblico e adattare le risposte di conseguenza. Assicurarsi dell'Accuratezza della Deviazione Standard Dati Mancanti: Dati mancanti possono distorcere il calcolo della tua deviazione standard. Per evitare imprecisioni, puoi escludere le risposte incomplete o utilizzare tecniche di imputazione. Evitare Valori Anomali: Controllare i tuoi dati per errori o valori anomali è essenziale. Anche un'errata voce può alterare significativamente i risultati. Utilizzare gli strumenti di sondaggio di LimeSurvey può aiutarti a raccogliere dati accurati e utilizzabili che riflettano la vera variabilità. Comprendendo la deviazione standard, potrai ottenere preziosi approfondimenti sui risultati del tuo sondaggio, permettendoti non solo di interpretare i dati in modo più efficace, ma anche di prendere decisioni migliori basate su una comprensione più profonda di come si sentono, agiscono o pensano i tuoi rispondenti. Dopo aver determinato la deviazione standard, LimeSurvey ti consente di migliorare le tue domande, in modo da sfruttare al meglio il tuo sondaggio e i tuoi dati. Provalo oggi!