Стандартное отклонение: все, что вам нужно знать для опросов.

Представьте, что вы проводите опрос удовлетворенности клиентов для популярной сети кафе. Ожидаете, что большинство клиентов высоко оценят кофе, ведь ваше кафе славится качеством и отличным обслуживанием. Но когда вы смотрите на результаты, оценки разбросаны. Некоторые клиенты оставляют положительные отзывы, в то время как другие кажутся недовольными. В чем дело? Здесь на помощь приходит стандартное отклонение, позволяющее количественно оценить ваши данные и понять, насколько ответы согласованы или если они сильно различаются. С помощью этого метода вы можете выяснить, являются ли те немногие низкие оценки выбросами или предложения вашего бренда действительно непостоянны. Что такое стандартное отклонение? В своей основе стандартное отклонение измеряет, насколько разбросаны значения в наборе данных. Оно показывает, насколько индивидуальные ответы отклоняются от среднего, помогая понять, являются ли ваши данные последовательными или имеют значительные колебания. В анализе опросов стандартное отклонение дает более глубокие представления о том, как люди отвечают, что делает его ценным инструментом для интерпретации результатов. Например, если все ваши клиенты оценили ваше обслуживание на 8 или 9 из 10, у вас будет небольшое стандартное отклонение, что означает, что результаты довольно последовательны. С другой стороны, если некоторые оценивают на 2, а другие на 10, стандартное отклонение будет значительно больше, сигнализируя о более разнообразных мнениях. Символ стандартного отклонения — “σ” (маленькаяsigma) для популяционного стандартного отклонения и “sss” для стандартного отклонения выборки. Это сокращение, используемое в статистических уравнениях и формулах для обозначения изменчивости. Важность стандартного отклонения в опросах Стандартное отклонение предоставляет меру надежности ответов. Хотя среднее значение может дать вам быструю сводку, стандартное отклонение добавляет контекст. Оно показывает, сгруппированы ли большинство ответов вокруг этого среднего или разбросаны по широкому диапазону. Небольшое стандартное отклонение предполагает последовательность, в то время как большое указывает на изменчивость — что может говорить о различиях в интерпретации или опыте. Эта мера позволяет исследователям и бизнесу увидеть глубже данные опросов, помогая определить области, в которых мнения расходятся, и в конечном итоге направляя более целенаправленные улучшения или изменения. Расчет стандартного отклонения шаг за шагом с примером Расчет стандартного отклонения может показаться сложным на первый взгляд, но это пошаговый процесс, который упрощается с практикой. Сначала вычислите среднее (среднее) вашего набора данных. Затем вычтите среднее из каждой точки данных, возведите результат в квадрат и найдите среднее этих квадратных отклонений. Наконец, возьмите квадратный корень из этого среднего, чтобы получить стандартное отклонение. 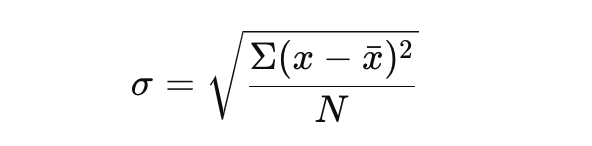Начнем с использования следующей формулы: Эта формула дает четкое представление о изменчивости вашего набора данных. Предположим, вы провели опрос, в котором 5 клиентов оценили свою удовлетворенность вашим обслуживанием по шкале от 1 до 10. Ответы были: 7, 8, 6, 9, 10. Теперь давайте вычислим стандартное отклонение для этого набора данных: Шаг 1: Найдите среднее (среднее значение) Чтобы найти среднее, сложите все точки данных и разделите на количество ответов. 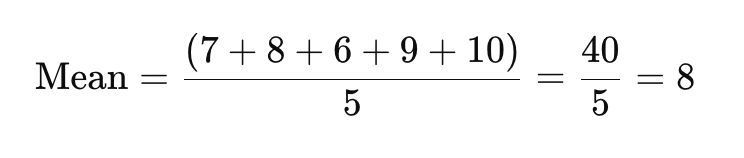Средняя оценка удовлетворенности здесь составляет 8. Шаг 2: Вычтите среднее из каждой точки данных и возведите результат в квадрат Затем для каждой оценки вычтите среднее (8), а затем возведите результат в квадрат. Это исключает отрицательные значения и подчеркивает отклонения. 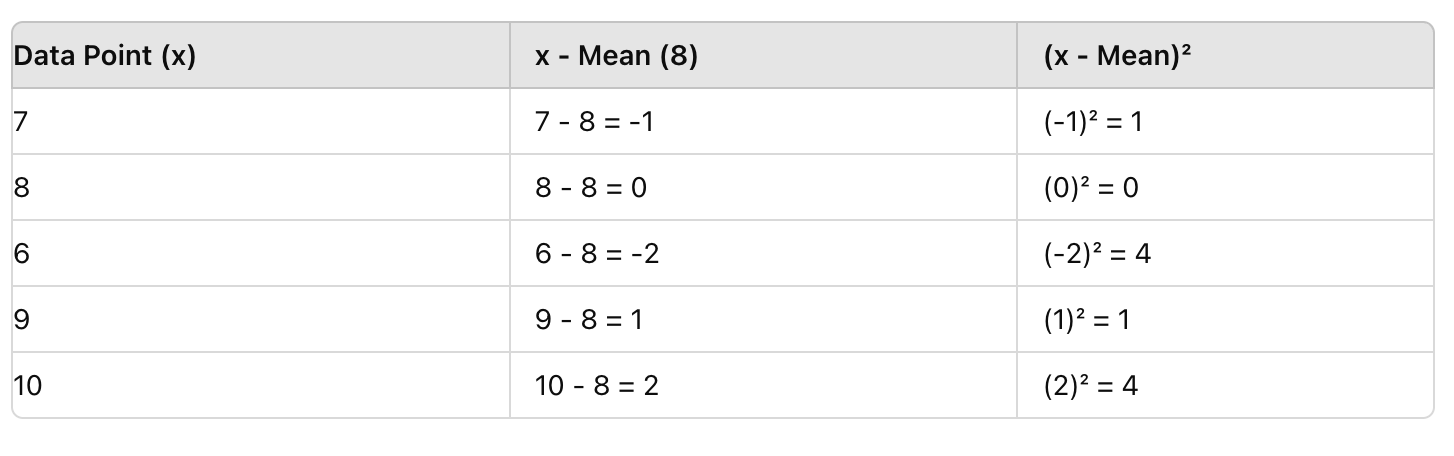Шаг 3: Найдите среднее квадратных отклонений Теперь сложите квадратные отклонения и разделите на количество точек данных, чтобы найти дисперсию. 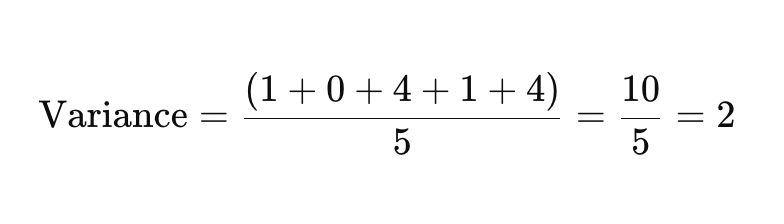Шаг 4: Возьмите квадратный корень дисперсии Наконец, возьмите квадратный корень дисперсии, чтобы найти стандартное отклонение. В этом примере стандартное отклонение составляет примерно 1.41. Это означает, что большинство оценок удовлетворенности клиентов находятся в пределах 1.41 пункта от средней оценки (8). Поскольку стандартное отклонение относительно небольшое, оценки довольно близки к среднему, что указывает на последовательность отзывов. Если бы стандартное отклонение было больше, скажем, 3 или 4, это бы указывало на более широкий разброс ответов, при этом некоторые клиенты были бы намного более или менее удовлетворены, чем другие. Стандартное отклонение в Excel Пошаговое руководство по использованию Excel для стандартного отклонения Microsoft Excel или Google Sheets — одно из самых удобных средств для расчета стандартного отклонения. Вот как это сделать: Введите ваши данные в столбец. Выберите пустую ячейку, где вы хотите увидеть результат. Используйте формулу =STDEV.P() для популяционного стандартного отклонения или =STDEV.S() для стандартного отклонения выборки. Выделите свои данные, нажмите Enter, и Excel мгновенно посчитает результат. Excel автоматизирует процесс, экономя время и уменьшая вероятность ошибок. Экспорт данных LimeSurvey в Excel С помощью LimeSurvey вы можете экспортировать данные опроса напрямую в Excel для дальнейшего анализа результатов. Для этого: Перейдите в раздел результатов в LimeSurvey. Выберите опцию экспорта и выберите формат Excel. После экспорта используйте статистические функции Excel, включая стандартное отклонение, чтобы глубже понять данные. Совмещая возможности сбора данных LimeSurvey с инструментами анализа Excel, вы можете эффективно интерпретировать и действовать по результатам опроса. Понимание стандартного отклонения Стандартное отклонение vs. стандартная ошибка Стандартное отклонение и стандартная ошибка связаны, но служат разным целям. Стандартное отклонение измеряет разброс отдельных точек данных, тогда как стандартная ошибка измеряет точность среднеарифметического выборки по сравнению с истинным среднеарифметическим по популяции. В опросах стандартное отклонение помогает понять изменчивость ответов, в то время как стандартная ошибка полезна для оценки того, насколько близко ваше среднее значение выборки к истинному среднему значению популяции. Стандартное отклонение vs. дисперсия Дисперсия — это еще одна мера разброса данных и является квадратом стандартного отклонения. Хотя дисперсия помогает количественно оценить величину изменчивости, стандартное отклонение легче интерпретировать, так как оно выражается в тех же единицах, что и ваши исходные данные. Например, если вы измеряете оценки удовлетворенности, стандартное отклонение даст интуитивное понимание того, насколько сильно ответы отличаются от среднего. Интерпретация результатов стандартного отклонения После того как вы рассчитали стандартное отклонение, вы можете использовать его для интерпретации последовательности ваших опросных ответов. Низкое стандартное отклонение означает, что респонденты в целом согласны, в то время как высокое стандартное отклонение сигнализирует о различных мнениях. Например, представьте, что вы опросили 100 сотрудников о их удовлетворенности работой по шкале от 1 до 10. Если большинство ответов сгруппированы вокруг 8, с небольшим стандартным отклонением, это указывает на общую удовлетворенность. Однако, если оценки варьируются от 4 до 10, большее стандартное отклонение показывает, что мнения более разделены, и вам может потребоваться дальнейшее расследование. Практическое применение стандартного отклонения Улучшение вопросов опроса: Если вы заметили большое стандартное отклонение по конкретному вопросу опроса, это может указывать на то, что вопрос неоднозначен или плохо понятен респондентам. Уточнение формулировки может помочь собрать более точные данные в будущих опросах. Принятие решений на основе данных: Стандартное отклонение помогает принимать более обоснованные решения, выявляя закономерности в ваших данных опросов. Например, если отзывы сильно варьируются, вы можете сегментировать свою аудиторию и адаптировать ответы соответственно. Обеспечение точности стандартного отклонения Недостающие данные: Недостающие данные могут искажать ваши расчеты стандартного отклонения. Чтобы избежать неточностей, либо учтите недостающие данные, исключив неполные ответы, либо используйте методы импутации. Избегание выбросов: Дважды проверьте ваши данные на ошибки или выбросы. Даже одна неправильная запись может значительно изменить ваши результаты. Использование инструментов опроса LimeSurvey может помочь вам собрать точные, пригодные для использования данные, которые отражают истинную изменчивость. Понимание стандартного отклонения позволит вам раскрыть мощные идеи из результатов опроса. Это позволяет не только более эффективно интерпретировать данные, но и принимать лучшие решения на основе более глубокого понимания того, как ваши респонденты чувствуют, действуют или мыслят. После определения стандартного отклонения LimeSurvey позволяет вам улучшить ваши вопросы, чтобы вы могли максимально эффективно использовать свои опросы и данные. Попробуйте уже сегодня!