Odchylenie standardowe: wszystko, co musisz wiedzieć o badaniach.

Wyobraź sobie, że przeprowadzasz ankietę satysfakcji klientów w popularnej sieci kawiarni. Spodziewasz się, że większość klientów oceni kawę wysoko — w końcu Twoja kawiarnia szczyci się kontrolą jakości i doskonałą obsługą. Jednak gdy spojrzysz na wyniki, oceny są bardzo zróżnicowane. Niektórzy klienci wystawiają znakomite recenzje, podczas gdy inni wydają się mieć złe doświadczenia. Co się dzieje? W tym miejscu odchylenie standardowe pomaga w kwantyfikacji danych, umożliwiając zrozumienie, czy odpowiedzi są blisko siebie, czy też znacznie się różnią. Dzięki tej metodzie możesz odkryć, czy te kilka niskich ocen to wyjątki, czy wręcz przeciwnie — oferta Twojej marki jest naprawdę niespójna. Czym jest odchylenie standardowe? W swojej istocie odchylenie standardowe mierzy, jak rozproszone są wartości w zbiorze danych. Informuje, jak bardzo indywidualne odpowiedzi odbiegają od średniej, co pomaga zrozumieć, czy dane są spójne, czy mają znaczną zmienność. W analizie ankiet odchylenie standardowe dostarcza głębszych informacji na temat tego, jak ludzie odpowiadają, czyniąc je cennym narzędziem do interpretacji wyników. Na przykład, jeśli wszyscy klienci oceniają Twoją usługę na 8 lub 9 na 10, będziesz miał małe odchylenie standardowe, co oznacza, że wyniki są dość spójne. Z drugiej strony, jeśli niektórzy oceniają to na 2, a inni na 10, odchylenie standardowe będzie znacznie większe, co sygnalizuje zróżnicowane opinie. Symbol odchylenia standardowego to „σ” (mała sigma) dla odchylenia standardowego populacji, oraz „sss” dla odchylenia standardowego próbki. Jest to skrót używany w równaniach i formułach statystycznych do oznaczania zmienności. Znaczenie odchylenia standardowego w ankietach Odchylenie standardowe dostarcza miary niezawodności odpowiedzi. Podczas gdy średnia ocena może dać szybki przegląd, odchylenie standardowe dodaje kontekstu. Wskazuje, czy większość odpowiedzi skupia się wokół tej średniej, czy też jest rozproszona w szerokim zakresie. Małe odchylenie standardowe sugeruje spójność, podczas gdy duże wskazuje na zmienność — co może oznaczać różnice w interpretacji lub doświadczeniach. To pomiar pozwala badaczom i firmom dostrzegać więcej niż tylko powierzchnię danych z ankiet, pomagając identyfikować obszary, w których opinie się różnią, a ostatecznie prowadząc do bardziej ukierunkowanych ulepszeń lub zmian. Obliczanie odchylenia standardowego krok po kroku na przykładzie Obliczanie odchylenia standardowego może wydawać się skomplikowane na początku, ale jest to proces krok po kroku, który staje się łatwiejszy dzięki praktyce. Najpierw oblicz średnią (średnią arytmetyczną) swojego zestawu danych. Następnie odejmij średnią od każdego punktu danych, podnieś wynik do kwadratu i znajdź średnią tych kwadratowych różnic. Na koniec wyciągnij pierwiastek kwadratowy z tej średniej, aby uzyskać odchylenie standardowe. 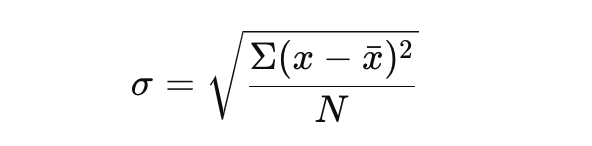Rozpocznijmy od użycia następującego wzoru: Ten wzór daje jasny obraz zmienności w zestawie danych. Załóżmy, że przeprowadziłeś ankietę, prosząc 5 klientów o ocenę satysfakcji z usługi w skali od 1 do 10. Odpowiedzi były następujące: 7, 8, 6, 9, 10. Obliczmy teraz odchylenie standardowe dla tego zestawu danych: Krok 1: Znajdź średnią Aby znaleźć średnią, dodaj wszystkie punkty danych i podziel przez liczbę odpowiedzi. 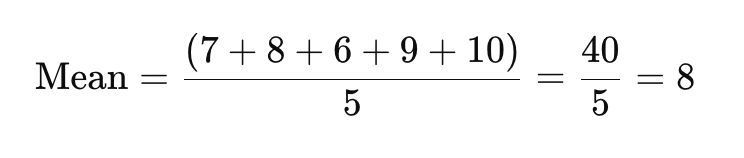Średnia ocena satysfakcji wynosi tutaj 8. 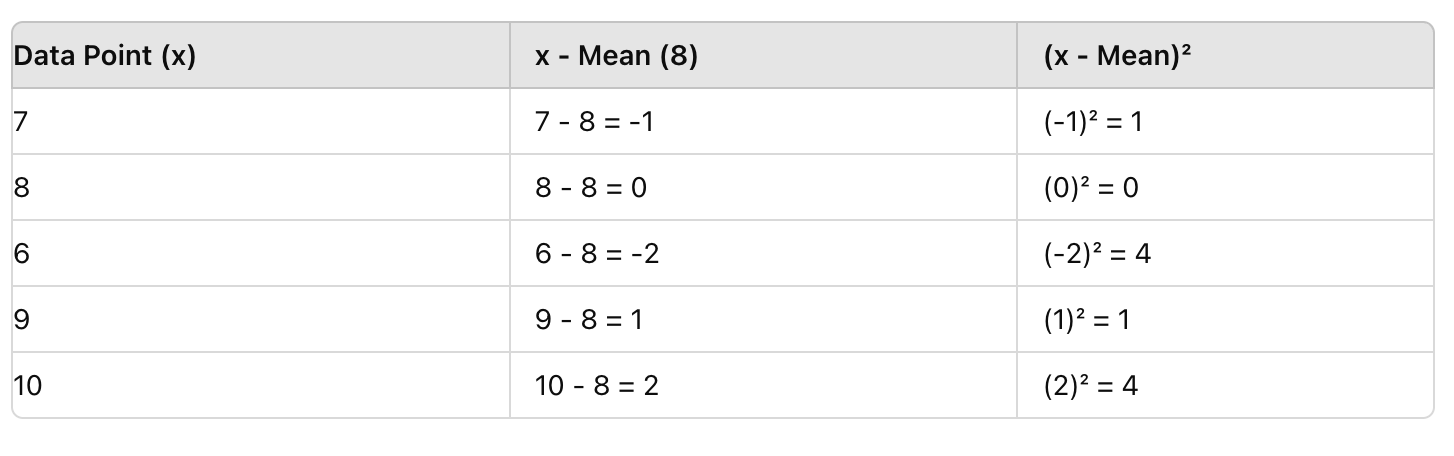Krok 2: Odejmij średnią od każdego punktu danych i podnieś wynik do kwadratu Następnie dla każdej oceny odejmij średnią (8), a następnie podnieś wynik do kwadratu. To usuwa wartości ujemne i podkreśla odchylenia. Krok 3: Znajdź średnią kwadratowych różnic Teraz dodaj kwadratowe różnice i podziel przez liczbę punktów danych, aby znaleźć wariancję. 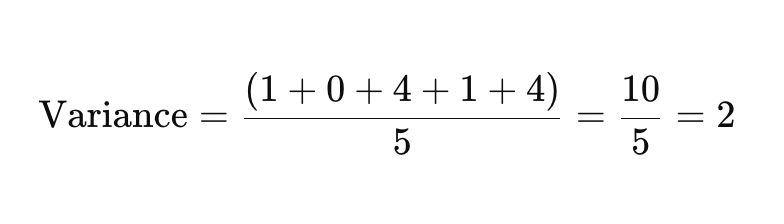Krok 4: Wyciągnij pierwiastek kwadratowy z wariancji Na koniec, wyciągnij pierwiastek kwadratowy z wariancji, aby znaleźć odchylenie standardowe. W tym przykładzie odchylenie standardowe wynosi około 1,41. Oznacza to, że większość ocen satysfakcji klientów mieści się w zakresie 1,41 punktów od średniej (8). Ponieważ odchylenie standardowe jest stosunkowo małe, oceny są dość bliskie średniej, co wskazuje na spójność w opiniach. Gdyby odchylenie standardowe było większe, na przykład 3 lub 4, sugerowałoby to szerszy rozkład odpowiedzi, z niektórymi klientami znacznie bardziej lub mniej zadowolonymi niż inni. Odchylenie standardowe w Excelu Krok po kroku, jak używać Excela do obliczenia odchylenia standardowego Microsoft Excel lub Google Sheets to jedne z najwygodniejszych narzędzi do obliczania odchylenia standardowego. Oto jak to zrobić: Wpisz swoje dane w kolumnie. Wybierz pustą komórkę, w której chcesz uzyskać wynik. Użyj wzoru =STDEV.P() dla odchylenia standardowego populacji lub =STDEV.S() dla odchylenia standardowego próbki. Podświetl swoje dane, naciśnij Enter, a Excel natychmiast obliczy wynik. Excel automatyzuje proces, oszczędzając czas i zmniejszając ryzyko błędów manualnych. Eksportowanie danych z LimeSurvey do Excela W LimeSurvey możesz eksportować dane z ankiety bezpośrednio do Excela, aby dokładniej analizować wyniki. Aby to zrobić: Przejdź do sekcji wyników w LimeSurvey. Wybierz opcję eksportu i wybierz format Excel. Po wyeksportowaniu skorzystaj z funkcji statystycznych Excela, w tym odchylenia standardowego, aby uzyskać głębsze zrozumienie swoich danych. Dzięki połączeniu możliwości zbierania danych LimeSurvey z narzędziami analitycznymi Excela, możesz efektywnie interpretować i działać na podstawie wyników ankiety. Zrozumienie odchylenia standardowego Odchylenie standardowe a błąd standardowy Odchylenie standardowe i błąd standardowy są ze sobą powiązane, ale służą różnym celom. Odchylenie standardowe mierzy rozrzut indywidualnych punktów danych, podczas gdy błąd standardowy mierzy dokładność średniej próbki w porównaniu do rzeczywistej średniej populacji. W ankietach odchylenie standardowe pomaga zrozumieć zmienność odpowiedzi, podczas gdy błąd standardowy jest użyteczny do oszacowania, jak blisko średnia próbki jest do rzeczywistej średniej populacji. Odchylenie standardowe a wariancja Wariancja to kolejna miara rozproszenia danych i jest kwadratem odchylenia standardowego. Podczas gdy wariancja pomaga kwantyfikować wielkość zmienności, odchylenie standardowe jest łatwiejsze do interpretacji, ponieważ jest wyrażone w tych samych jednostkach, co oryginalne dane. Na przykład, jeśli mierzysz oceny satysfakcji, odchylenie standardowe dostarczy intuicyjnego zrozumienia, jak bardzo odpowiedzi różnią się od średniej. Interpretacja wyników odchylenia standardowego Po obliczeniu odchylenia standardowego możesz użyć go do interpretacji spójności odpowiedzi w ankiecie. Niskie odchylenie standardowe oznacza, że respondenci są generalnie zgodni, podczas gdy wysokie odchylenie standardowe sygnalizuje zróżnicowane opinie. Na przykład, wyobraź sobie, że przeprowadziłeś ankietę z 100 pracownikami na temat ich satysfakcji z pracy w skali od 1 do 10. Jeśli większość odpowiedzi koncentruje się wokół 8, z małym odchyleniem standardowym, sugeruje to ogólne zadowolenie. Jednak jeśli oceny wahają się od 4 do 10, większe odchylenie standardowe pokazuje, że opinie są bardziej podzielone, co może wymagać dalszego zbadania. Praktyczne zastosowania odchylenia standardowego Udoskonalanie pytań ankietowych: Jeśli zauważysz duże odchylenie standardowe dla konkretnego pytania ankietowego, może to wskazywać, że pytanie jest niejasne lub źle zrozumiane przez respondentów. Udoskonalenie sformułowania może pomóc w uzyskaniu dokładniejszych danych w przyszłych ankietach. Podejmowanie decyzji opartych na danych: Odchylenie standardowe pomaga podejmować bardziej świadome decyzje, ujawniając wzorce w danych z ankiet. Na przykład, jeśli opinie są bardzo zróżnicowane, możesz podzielić swoją publiczność na segmenty i dostosować odpowiedzi odpowiednio. Zapełnienie dokładności w odchyleniu standardowym Brakujące dane: Brakujące dane mogą zniekształcić obliczenia odchylenia standardowego. Aby uniknąć nieścisłości, należy albo uwzględnić brakujące dane, wykluczając niepełne odpowiedzi, albo zastosować techniki imputacji. Unikanie wartości odstających: Sprawdzenie danych pod kątem błędów lub wartości odstających jest niezbędne. Nawet jeden błędny wpis może znacząco wpłynąć na wyniki. Używanie narzędzi ankietowych LimeSurvey może pomóc w zbieraniu dokładnych danych, które odzwierciedlają rzeczywistą zmienność. Rozpoczynając od zrozumienia odchylenia standardowego, odkryjesz potężne spostrzeżenia dotyczące wyników swojej ankiety. Pozwoli to nie tylko lepiej interpretować dane, ale także podejmować lepsze decyzje na podstawie głębszego zrozumienia tego, jak czują się, działają lub myślą Twoi respondenci. Po określeniu odchylenia standardowego LimeSurvey pozwala Ci poprawić swoje pytania, abyś mógł maksymalnie wykorzystać swoją ankietę i dane. Spróbuj już dziś!