Tabelinhoud

Stel je voor dat je een klanttevredenheidsonderzoek uitvoert voor een populaire caféketen. Je verwacht dat de meeste klanten de koffie hoog waarderen, omdat jouw café trots is op kwaliteitscontrole en uitstekende service. Maar als je naar de resultaten kijkt, zijn de beoordelingen erg wisselend. Sommige klanten geven lovende reviews, terwijl anderen een slechte ervaring lijken te hebben. Wat is er aan de hand?

Hier komt de standaarddeviatie om de hoek kijken; deze helpt om je gegevens te kwantificeren en te begrijpen of de reacties dicht bij elkaar liggen of sterk variëren. Met deze methode kun je achterhalen of die paar lage cijfers uitzonderingen zijn, of dat de aanbiedingen van je merk werkelijk inconsistent zijn.

Wat is Standaarddeviatie?

Standaarddeviatie meet hoe verspreid de waarden in een dataset zijn. Het geeft aan hoeveel individuele reacties afwijken van het gemiddelde, wat je helpt te begrijpen of je gegevens consistent zijn of significante variabiliteit vertonen. In enquêteanalyse biedt standaarddeviatie diepere inzichten in hoe mensen reageren, waardoor het een waardevol hulpmiddel is voor het interpreteren van resultaten.

Bijvoorbeeld, als al je klanten je service een 8 of 9 geven, heb je een kleine standaarddeviatie, wat betekent dat de resultaten redelijk consistent zijn. Aan de andere kant, als sommigen een 2 en anderen een 10 geven, zal de standaarddeviatie veel groter zijn, wat duidt op meer diverse meningen.

Het symbool voor standaarddeviatie is “σ” (kleine sigma) voor de standaarddeviatie van de populatie en “sss” voor de standaarddeviatie van de steekproef. Het is een afkorting die in statistische vergelijkingen en formules wordt gebruikt om variabiliteit aan te duiden.

Het Belang van Standaarddeviatie in Enquêtes

Standaarddeviatie biedt een maat voor de betrouwbaarheid van de reacties. Terwijl de gemiddelde score je een snel overzicht geeft, voegt standaarddeviatie context toe. Het laat zien of de meeste reacties rond dat gemiddelde zijn gegroepeerd of dat ze over een breed scala zijn verspreid. Een kleine standaarddeviatie suggereert consistentie, terwijl een grote wijst op variabiliteit, wat kan duiden op verschillen in interpretatie of ervaring.

Deze meting stelt onderzoekers en bedrijven in staat om verder te kijken dan het oppervlak van enquêtegegevens, waardoor ze gebieden kunnen identificeren waar meningen uiteenlopen en uiteindelijk gerichte verbeteringen of veranderingen kunnen aanbrengen.

Standaarddeviatie Berekenen Stap voor Stap, met een Voorbeeld

Standaarddeviatie berekenen lijkt in het begin misschien complex, maar het is een stap-voor-stap proces dat eenvoudiger wordt met de oefening. Bereken eerst het gemiddelde van je dataset. Trek vervolgens het gemiddelde van elke datapunt af, kwadrateer het resultaat en vind het gemiddelde van deze kwadratische afwijkingen. Neem tenslotte de vierkantswortel van dit gemiddelde om de standaarddeviatie te berekenen.

Laten we beginnen met de volgende formule:

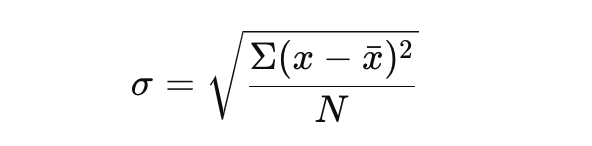
standaarddeviatie berekenen

Deze formule geeft je een duidelijk beeld van de variabiliteit in jouw dataset.

Stel dat je een enquête hebt gehouden waarbij 5 klanten gevraagd werden hun tevredenheid over de service te beoordelen op een schaal van 1 tot 10. De reacties waren: 7, 8, 6, 9, 10.

Laten we nu de standaarddeviatie voor deze dataset berekenen:

Stap 1: Vind het Gemiddelde

Om het gemiddelde te vinden, tel je alle datapunten bij elkaar op en deel je door het aantal reacties.

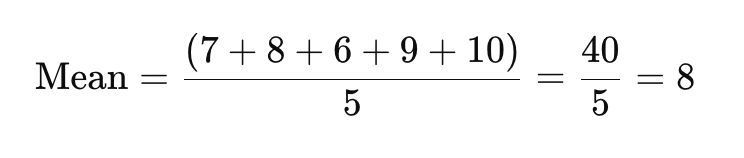
Gemiddelde vinden

De gemiddelde tevredenheidsscore hier is 8.

Stap 2: Trek het Gemiddelde van Elk Datapunt Af en Kwadrateer het Resultaat

Vervolgens trek je voor elke score het gemiddelde (8) af en kwadrateer je het resultaat. Dit verwijdert negatieve waarden en benadrukt afwijkingen.

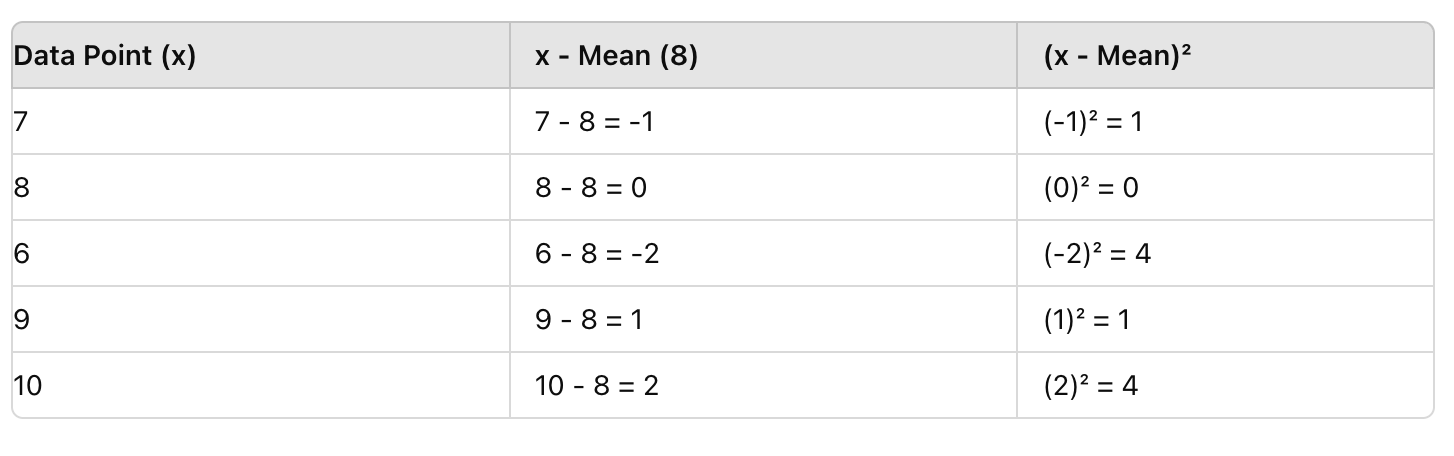
Trek het gemiddelde van elk datapunt af

Stap 3: Vind het Gemiddelde van de Kwadratische Verschillen

Voeg nu de gekwadrateerde verschillen bij elkaar op en deel je door het aantal datapunten om de variantie te vinden.

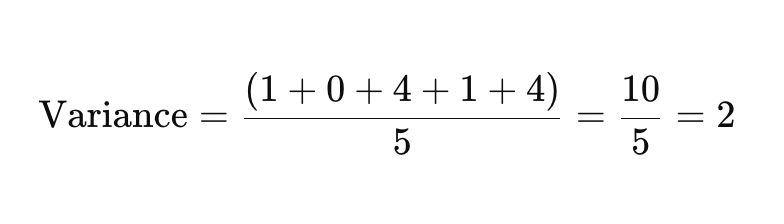
Gemiddelde van de kwadratische verschillen vinden

Stap 4: Neem de Vierkantswortel van de Variantie

Neem tenslotte de vierkantswortel van de variantie om de standaarddeviatie te vinden.

Neem de vierkantswortel van de variantie

In dit voorbeeld is de standaarddeviatie ongeveer 1.41. Dit betekent dat de meeste klanttevredenheidsscores binnen 1.41 punten van de gemiddelde score (8) liggen. Aangezien de standaarddeviatie relatief klein is, liggen de beoordelingen redelijk dicht bij het gemiddelde, wat op consistentie in de feedback wijst.

Als de standaarddeviatie groter zou zijn, laten we zeggen 3 of 4, zou dit een bredere spreiding van reacties suggereren, met sommige klanten die veel meer of minder tevreden zijn dan anderen.

Standaarddeviatie in Excel

Stapsgewijze Handleiding voor het Gebruik van Excel voor Standaarddeviatie

Microsoft Excel of Google Sheets is een van de handigste tools voor het berekenen van standaarddeviatie. Zo doe je dat:

  1. Voer je gegevens in een kolom in.
  2. Selecteer een lege cel waar je het resultaat wilt hebben.
  3. Gebruik de formule =STDEV.P() voor standaarddeviatie van de populatie of =STDEV.S() voor standaarddeviatie van de steekproef.
  4. Markeer je gegevens, druk op Enter, en Excel berekent het resultaat onmiddellijk.

Excel automatiseert het proces, bespaart je tijd en vermindert de kans op handmatige fouten.

Exporteren van LimeSurvey Gegevens naar Excel

Met LimeSurvey kun je je enquêtegegevens rechtstreeks naar Excel exporteren om je resultaten verder te analyseren. Om dit te doen:

  1. Ga naar de resultatensectie in LimeSurvey.
  2. Kies de exportoptie en selecteer Excel als formaat.
  3. Gebruik daarna de statistische functies van Excel, inclusief standaarddeviatie, om een dieper begrip van je gegevens te krijgen.

Door de dataverzamelingsmogelijkheden van LimeSurvey te combineren met de analysetools van Excel, kun je efficiënt je enquête-resultaten interpreteren en daarop actie ondernemen.

Begrijpen van Standaarddeviatie

  • Standaarddeviatie vs. Standaardfout
    Standaarddeviatie en standaardfout zijn gerelateerd, maar dienen verschillende doelen. Standaarddeviatie meet de spreiding van individuele datapunten, terwijl standaardfout de nauwkeurigheid van het steekproefgemiddelde ten opzichte van het ware populatiegemiddelde meet. In enquêtes helpt standaarddeviatie je de variabiliteit in de reacties te begrijpen, terwijl standaardfout nuttig is voor het schatten van hoe dicht je steekproefgemiddelde bij het daadwerkelijke populatiegemiddelde ligt.
  • Standaarddeviatie vs. Variantie
    Variantie is een andere maat voor gegevensverspreiding en is het kwadraat van de standaarddeviatie. Terwijl variantie helpt de omvang van de variabiliteit te kwantificeren, is standaarddeviatie gemakkelijker te interpreteren omdat deze wordt uitgedrukt in dezelfde eenheden als je oorspronkelijke gegevens. Bijvoorbeeld, als je tevredenheidsscores meet, zal standaarddeviatie een intuïtief begrip geven van hoezeer de reacties verschillen van het gemiddelde.

Interpreteren van Standaarddeviatie Resultaten

Eenmaal berekend, kun je de standaarddeviatie gebruiken om de consistentie van je enquête-antwoorden te interpreteren. Een lage standaarddeviatie betekent dat de respondenten over het algemeen het eens zijn, terwijl een hoge standaarddeviatie wijst op uiteenlopende meningen.

Bijvoorbeeld, stel dat je 100 werknemers hebt ondervraagd over hun werktevredenheid op een schaal van 1 tot 10. Als de meeste reacties rond de 8 zijn gegroepeerd, met een kleine standaarddeviatie, suggereert dit algemene tevredenheid. Echter, als de scores variëren van 4 tot 10, toont de grotere standaarddeviatie aan dat de meningen meer verdeeld zijn, en dat je wellicht verder moet onderzoeken.

Praktische Toepassingen van Standaarddeviatie

  • Verbeteren van Enquêtevragen: Als je een hoge standaarddeviatie voor een specifieke enquêtevraag opmerkt, kan dit duiden op onduidelijkheid of dat respondenten de vraag niet goed begrijpen. Het verfijnen van de formulering kan helpen om nauwkeurigere gegevens in toekomstige enquêtes te verzamelen.
  • Datagestuurde Beslissingen Nemen: Standaarddeviatie helpt je om meer geïnformeerde beslissingen te nemen door patronen in je enquêtegegevens bloot te leggen. Bijvoorbeeld, als de feedback zeer variabel is, kun je je publiek segmenteren en de reacties dienovereenkomstig aanpassen.

Zorg Voor Nauwkeurigheid in Standaarddeviatie

  • Ontbrekende Gegevens: Ontbrekende gegevens kunnen je berekening van standaarddeviatie verstoren. Om onnauwkeurigheden te voorkomen, kun je ofwel rekening houden met ontbrekende gegevens door onvolledige reacties uit te sluiten of imputatietechnieken gebruiken.
  • Uitzonderingen Vermijden: Het is essentieel om je gegevens te controleren op fouten of uitschieters. Zelfs één verkeerde invoer kan je resultaten aanzienlijk beïnvloeden. Het gebruik van de enquête-tools van LimeSurvey kan je helpen om nauwkeurige, bruikbare gegevens te verzamelen die ware variabiliteit weerspiegelen.

Door te beginnen met een begrip van standaarddeviatie, zul je krachtige inzichten in je enquête-resultaten ontsluiten. Dit stelt je in staat om de gegevens niet alleen effectiever te interpreteren, maar ook betere beslissingen te nemen op basis van een dieper begrip van hoe je respondenten zich voelen, handelen of denken.

Nadat je de standaarddeviatie hebt vastgesteld, stelt LimeSurvey je in staat om je vragen te verbeteren, zodat je het meeste uit je enquête en gegevens kunt halen.