Standardafvigelse: alt, hvad du behøver at vide til undersøgelser.

Forestil dig, at du gennemfører en kundetilfredshedsundersøgelse for en populær cafékæde. Du forventer, at de fleste kunder vurderer kaffen højt - din café er kendt for kvalitet og fremragende service. Men når du ser på resultaterne, er vurderingerne vidt spredte. Nogle kunder giver strålende anmeldelser, mens andre har haft en dårlig oplevelse. Hvad sker der? Her kommer standardafvigelse ind i billedet og hjælper med at kvantificere dine data, så du kan forstå, om svarene er tæt på gennemsnittet eller varierer meget. Denne metode kan afsløre, om de få lave scores er outliers, eller om dit brands tilbud faktisk er inkonsekvente. Hvad er Standardafvigelse? Standardafvigelse måler, hvor spredte værdierne i et datasæt er. Den viser, hvor meget individuelle svar afviger fra gennemsnittet, hvilket hjælper dig med at forstå, om dine data er konsistente eller har betydelig variabilitet. I undersøgelsesanalyse giver standardafvigelse dybere indsigt i, hvordan folk svarer, hvilket gør den til et værdifuldt redskab til at fortolke resultaterne. For eksempel, hvis alle dine kunder vurderer din service til 8 eller 9 ud af 10, vil du have en lille standardafvigelse, hvilket betyder, at resultaterne er ret konsistente. Omvendt, hvis nogle vurderer det til 2 og andre til 10, vil standardafvigelsen være meget større, hvilket signalerer mere forskellige meninger. Symbolet for standardafvigelse er “σ” (lille sigma) for populationsstandardafvigelse og “sss” for stikprøvestandardafvigelse. Det er en forkortelse, der anvendes i statistiske formler for at angive variabilitet. Betydningen af Standardafvigelse i Undersøgelser Standardafvigelse giver et mål for pålidelighed i svarene. Mens gennemsnittet (eller den gennemsnitlige score) kan give et hurtigt overblik, tilføjer standardafvigelse kontekst. Den viser, om de fleste svar ligger tæt på gennemsnittet eller er spredt over et bredt område. En lille standardafvigelse tyder på konsistens, mens en stor en peger på variabilitet - hvilket kan indikere forskelle i fortolkning eller erfaring. Dette mål gør det muligt for forskere og virksomheder at se forbi overfladen af undersøgelsesdata og hjælpe dem med at identificere områder, hvor meningerne divergerer, og i sidste ende guide mere målrettede forbedringer eller ændringer. Beregn Standardafvigelse Trin-for-Trin med et Eksempel At beregne standardafvigelse kan virke komplekst i starten, men det er en trin-for-trin proces, der bliver lettere med øvelse. Først beregnes gennemsnittet for dit datasæt. Derefter trækkes gennemsnittet fra hver datapunkt, resultatet kvadreres, og gennemsnittet af disse kvadrerede forskelle findes. Til sidst tages kvadratroden af dette gennemsnit for at få standardafvigelsen. 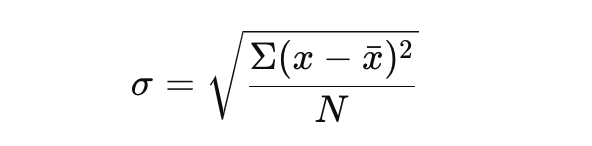Lad os begynde med at bruge følgende formel: Denne formel giver et klart billede af variabiliteten i dit datasæt. Lad os sige, at du har gennemført en undersøgelse, hvor 5 kunder blev bedt om at vurdere deres tilfredshed med din service på en skala fra 1 til 10. Svarene var: 7, 8, 6, 9, 10. Nu lad os beregne standardafvigelsen for dette datasæt: Trin 1: Find Gennemsnittet For at finde gennemsnittet, læg alle datapunkterne sammen og del med antallet af svar. 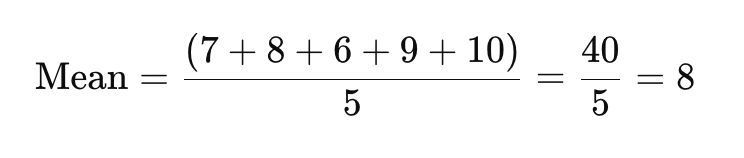Gennemsnitsvurderingen her er 8. Trin 2: Træk Gennemsnittet fra Hvert Datapunkt og Kvadrer Resultatet Næste skridt er at trække gennemsnittet (8) fra hver score og derefter kvadrere resultatet. Dette fjerner negative værdier og fremhæver afvigelser. 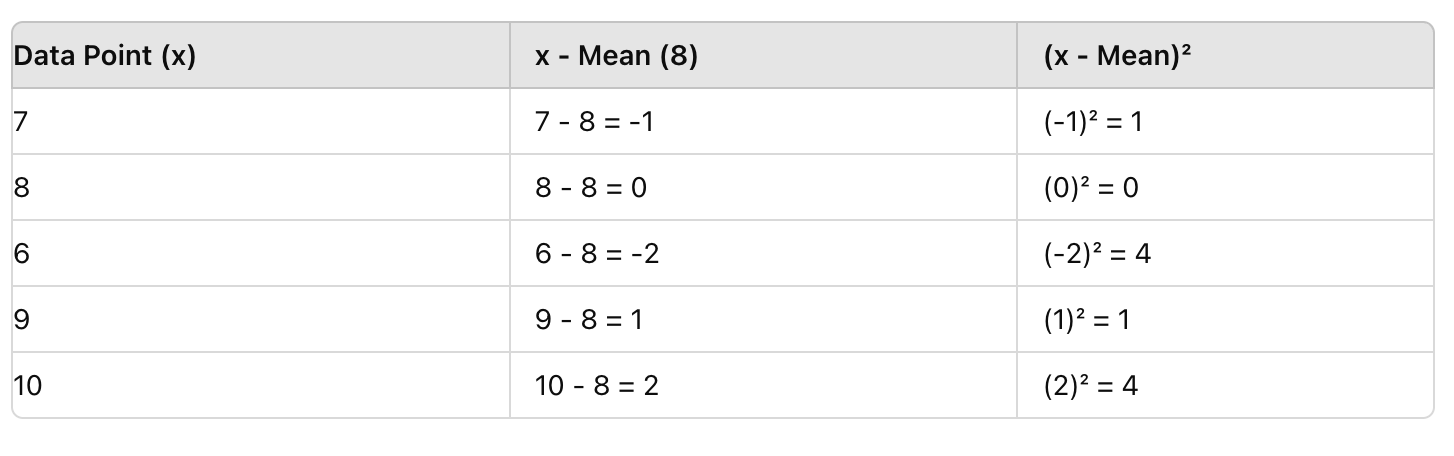Trin 3: Find Gennemsnittet af de Kvadrerede Forskelle Nu skal du lægge de kvadrerede forskelle sammen og dividere med antallet af datapunkter for at finde variansen. 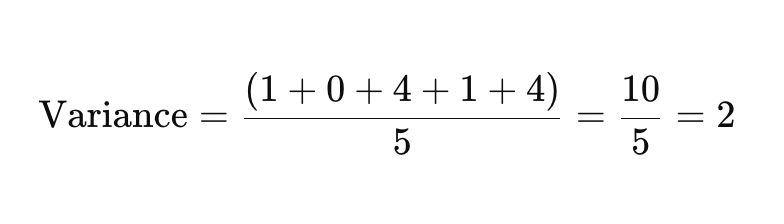Trin 4: Tag Kvadratroden af Variansen Til sidst tages kvadratroden af variansen for at finde standardafvigelsen. I dette eksempel er standardafvigelsen cirka 1,41. Det betyder, at de fleste kundetilfredsheds score ligger inden for 1,41 point fra gennemsnitsvurderingen (8). Da standardafvigelsen er relativt lille, er vurderingerne ret tæt på gennemsnittet, hvilket indikerer konsistens i feedbacken. Hvis standardafvigelsen var større, for eksempel 3 eller 4, ville det tyde på en bredere spredning af svar, hvor nogle kunder var meget mere eller mindre tilfredse end andre. Standardafvigelse i Excel Trin-for-Trin Guide til Brug af Excel for Standardafvigelse Microsoft Excel eller Google Sheets er et af de mest bekvemme værktøjer til at beregne standardafvigelse. Sådan gør du: Indtast dine data i en kolonne. Vælg en tom celle, hvor du vil have resultatet. Brug formlen =STDEV.P() for populationsstandardafvigelse eller =STDEV.S() for stikprøvestandardafvigelse. Marker dine data, tryk Enter, og Excel beregner straks resultatet. Excel automatiserer processen, sparer tid og reducerer risikoen for menneskelige fejl. Eksport af LimeSurvey Data til Excel Med LimeSurvey kan du eksportere dine undersøgelsesdata direkte til Excel for at analysere dine resultater. For at gøre dette: Naviger til resultatssektionen i LimeSurvey. Vælg eksportmuligheden og vælg Excel som format. Når det er eksporteret, kan du bruge Excels statistiske funktioner, herunder standardafvigelse, for at få en dybere forståelse af dine data. Ved at kombinere LimeSurvey's dataindsamlingsmuligheder med Excels analyseværktøjer kan du effektivt fortolke og handle på dine undersøgelsesresultater. Forståelse af Standardafvigelse Standardafvigelse vs. StandardfejlStandardafvigelse og standardfejl er relaterede, men tjener forskellige formål. Standardafvigelse måler spredningen af individuelle datapunkter, mens standardfejl måler nøjagtigheden af stikprøvegennemsnittet i forhold til den sande populationsgennemsnit. I undersøgelser hjælper standardafvigelse med at forstå variabiliteten i svarene, mens standardfejl er nyttig til at estimere, hvor tæt dit stikprøvegennemsnit er på det faktiske populationsgennemsnit. Standardafvigelse vs. VariansVarians er et andet mål for dataspredning og er kvadratet af standardafvigelsen. Mens varians hjælper med at kvantificere størrelsen af variabiliteten, er standardafvigelse lettere at fortolke, fordi den udtrykkes i de samme enheder som dine oprindelige data. For eksempel, hvis du måler tilfredsheds score, vil standardafvigelse give en intuitiv forståelse af, hvor meget svarene adskiller sig fra gennemsnittet. Fortolkning af Standardafvigelsesresultater Når du har beregnet standardafvigelsen, kan du bruge den til at fortolke konsistensen af dine undersøgelsesbesvarelser. En lav standardafvigelse betyder, at respondenterne generelt er enige, mens en høj standardafvigelse signalerer varierende meninger. For eksempel, forestil dig, at du har spurgt 100 medarbejdere om deres jobtilfredshed på en skala fra 1 til 10. Hvis de fleste svar ligger tæt på 8, med en lille standardafvigelse, antyder det generel tilfredshed. Men hvis vurderingerne spænder fra 4 til 10, viser den større standardafvigelse, at meningerne er mere delte, og du muligvis skal undersøge nærmere. Praktiske Anvendelser af Standardafvigelse Forbedring af Undersøgelsesspørgsmål: Hvis du bemærker en stor standardafvigelse for et specifikt spørgmål, kan det indikere, at spørgsmålet er tvetydigt eller ikke er godt forstået af respondenterne. At forbedre formuleringen kan hjælpe med at indsamle mere præcise data i fremtidige undersøgelser. Beslutningstagning baseret på data: Standardafvigelse hjælper dig med at træffe mere informerede beslutninger ved at afsløre mønstre i dine undersøgelsesdata. For eksempel, hvis feedback er meget variabel, kan du segmentere dit publikum og tilpasse svarene derefter. Sikring af Nøjagtighed i Standardafvigelse Manglende Data: Manglende data kan forvrænge din beregning af standardafvigelse. For at undgå unøjagtigheder skal du enten tage højde for manglende data ved at udelukke ufuldstændige svar eller bruge imputationsmetoder. Undgå Outliers: Det er vigtigt at dobbeltkontrollere dine data for fejl eller outliers. Selv én forkert indtastning kan ændre dine resultater betydeligt. At bruge LimeSurvey's undersøgelsesværktøjer kan hjælpe dig med at indsamle nøjagtige, anvendelige data, der afspejler ægte variabilitet. Ved at starte med en forståelse af standardafvigelse vil du få adgang til kraftfulde indsigter i dine undersøgelsesresultater. Dette giver dig mulighed for ikke kun at fortolke dataene mere effektivt, men også træffe bedre beslutninger baseret på en dybere forståelse af, hvordan dine respondenter føler, handler eller tænker. Efter at have fastslået standardafvigelsen giver LimeSurvey dig mulighed for at forbedre dine spørgsmål, så du kan få det bedste ud af din undersøgelse og data. Prøv det i dag!