Štandardná odchýlka: všetko, čo potrebujete vedieť o prieskumoch.

Predstavte si, že prevádzate prieskum spokojnosti zákazníkov pre populárny reťazec kaviarní. Očakávate, že väčšina zákazníkov ohodnotí kávu vysoko – predsa len, vaša kaviareň si zakladá na kvalitnej kontrole a vynikajúcej službe. Ale keď sa pozriete na výsledky, hodnotenia sú úplne roztrhnuté. Niektorí zákazníci vás chvália, zatiaľ čo iní mali zlú skúsenosť. Čo sa deje? Tu prichádza na pomoc smerodajná odchýlka, ktorá kvantifikuje vaše dáta a umožňuje vám pochopiť, či sú odpovede blízko priemeru alebo sa výrazne líšia. S touto metódou môžete zistiť, či sú nízke hodnotenia výnimočné, alebo či sú ponuky vašej značky skutočne nekonzistentné. Čo je smerodajná odchýlka? Smerodajná odchýlka v podstate meria, ako sú hodnoty v súbore dát rozptýlené. Hovorí vám, ako veľmi sa jednotlivé odpovede líšia od priemeru, čím vám pomáha pochopiť, či sú vaše dáta konzistentné alebo majú významnú variabilitu. V analýze prieskumov vám smerodajná odchýlka poskytuje hlbšie pohľady na to, ako ľudia odpovedajú, čím sa stáva cenným nástrojom pre interpretáciu výsledkov. Napríklad, ak všetci vaši zákazníci ohodnotia vašu službu 8 alebo 9 z 10, máte malú smerodajnú odchýlku, čo znamená, že výsledky sú pomerne konzistentné. Naopak, ak niektorí hodnotia 2 a iní 10, smerodajná odchýlka bude oveľa väčšia, čo signalizuje rozmanité názory. Symbolom pre smerodajnú odchýlku je “σ” (malé sigma) pre smerodajnú odchýlku populácie a “sss” pre smerodajnú odchýlku vzorky. Je to skratka používaná v štatistických rovniciach a vzorcoch na označenie variability. Dôležitosť smerodajnej odchýlky v prieskumoch Smerodajná odchýlka poskytuje mieru spoľahlivosti v odpovediach. Zatiaľ čo priemer (alebo aritmetický priemer) môže poskytnúť rýchly súhrn, smerodajná odchýlka dodáva kontext. Ukazuje, či sú väčšina odpovedí sústredená okolo priemeru alebo sú rozptýlené v širokom rozmedzí. Malá smerodajná odchýlka naznačuje konzistentnosť, zatiaľ čo veľká poukazuje na variabilitu – čo môže naznačovať rozdiely v interpretácii alebo skúsenosti. Táto metóda umožňuje výskumníkom a firmám vidieť za povrch prieskumových dát, pomáhať identifikovať oblasti, kde sa názory líšia, a nakoniec navádzať na cielené zlepšenia alebo zmeny. Výpočet smerodajnej odchýlky krok za krokom, s príkladom Výpočet smerodajnej odchýlky sa na prvý pohľad môže zdať zložitý, ale je to krok za krokom proces, ktorý sa stáva jednoduchším s praxou. Najprv vypočítajte priemer (aritmetický priemer) vášho dátového súboru. Potom od každého bodu dát odpočítajte priemer, umocnite výsledok a nájdite priemer týchto umocnených rozdielov. Nakoniec zoberte druhú odmocninu tohto priemeru, aby ste získali smerodajnú odchýlku. 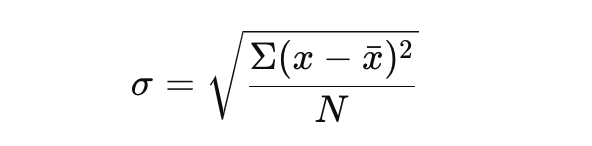Začnime použitím nasledujúceho vzorca: Tento vzorec vám poskytne jasný prehľad o variabilite vo vašom dátovom súbore. Povedzme, že ste uskutočnili prieskum, v ktorom 5 zákazníkov hodnotilo svoju spokojnosť so službou na stupnici od 1 do 10. Odpovede boli: 7, 8, 6, 9, 10. Teraz si vypočítajme smerodajnú odchýlku pre tento dátový súbor: Krok 1: Nájdite priemer (aritmetický priemer) Aby ste našli priemer, sčítajte všetky body dát a vydelte počtom odpovedí. 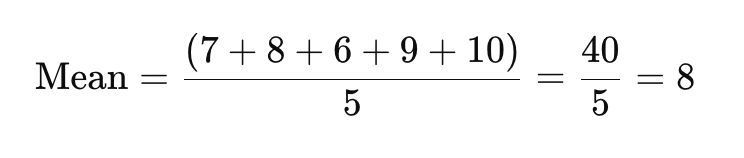Priemerné hodnotenie spokojnosti tu je 8. Krok 2: Odpočítajte priemer od každého bodu dát a umocnite výsledok Ďalej, pre každé hodnotenie odpočítajte priemer (8), potom umocnite výsledok. Tým sa odstráni negatívne hodnoty a zdôraznia sa odchýlky. 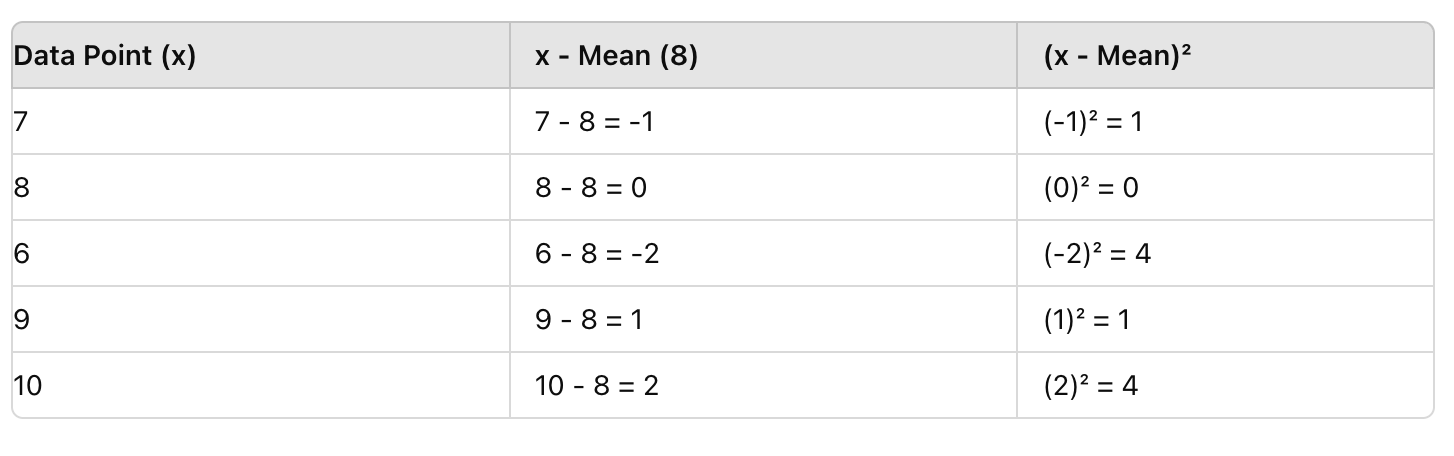Krok 3: Nájdite priemer umocnených rozdielov Teraz sčítajte umocnené rozdiely a vydelte počtom bodov dát, aby ste našli rozptyl. 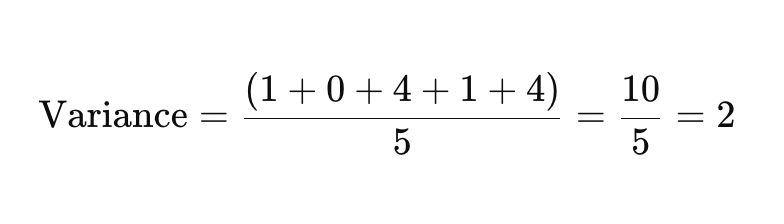Krok 4: Zoberte druhú odmocninu rozptylu Na záver zoberte druhú odmocninu rozptylu, aby ste našli smerodajnú odchýlku. V tomto príklade je smerodajná odchýlka približne 1,41. To znamená, že väčšina hodnotení spokojnosti zákazníkov je v rámci 1,41 bodu od priemerného skóre (8). Keďže smerodajná odchýlka je relatívne malá, hodnotenia sú pomerne blízko priemeru, čo naznačuje konzistentnosť v spätných väzbách. Keby bola smerodajná odchýlka väčšia, povedzme 3 alebo 4, naznačovalo by to širšie rozloženie odpovedí, pričom niektorí zákazníci by boli oveľa spokojnejší alebo nespokojnejší ako ostatní. Smerodajná odchýlka v Exceli Krok za krokom návod na použitie Excelu pre smerodajnú odchýlku Microsoft Excel alebo Google Sheets je jedným z najpohodlnejších nástrojov na výpočet smerodajnej odchýlky. Tu je návod, ako to urobiť: Zadajte svoje dáta do stĺpca. Vyberte prázdnu bunku, kde chcete výsledok. Použite vzorec =STDEV.P() pre smerodajnú odchýlku populácie alebo =STDEV.S() pre smerodajnú odchýlku vzorky. Označte svoje údaje, stlačte Enter a Excel okamžite vypočíta výsledok. Excel automatizuje proces, šetrí váš čas a znižuje riziko manuálnych chýb. Exportovanie dát LimeSurvey do Excelu Pomocou LimeSurvey môžete exportovať svoje prieskumové dáta priamo do Excelu na ďalšiu analýzu výsledkov. Ak to chcete urobiť: Prejdite na sekciu výsledkov v LimeSurvey. Vyberte možnosť exportu a zvoľte Excel ako formát. Akonáhle je export hotový, použite Excelove štatistické funkcie, vrátane smerodajnej odchýlky, na hlbšie pochopenie svojich dát. Kombinovaním schopností zberu dát LimeSurvey so štatistickými nástrojmi Excelu môžete efektívne interpretovať a konať na základe výsledkov svojho prieskumu. Pochopenie smerodajnej odchýlky Smerodajná odchýlka vs. štandardná chyba Smerodajná odchýlka a štandardná chyba sú príbuzné, ale slúžia na rôzne účely. Smerodajná odchýlka meria rozptýlenie jednotlivých dátových bodov, zatiaľ čo štandardná chyba meria presnosť priemerného vzorky v porovnaní so skutočným priemerom populácie. V prieskumoch smerodajná odchýlka pomáha pochopiť variabilitu odpovedí, kým štandardná chyba je užitočná na odhad, ako blízko je váš priemer vzorky k skutočnému priemeru populácie. Smerodajná odchýlka vs. rozptyl Rozptyl je ďalší mierou disperzie dát a je druhou mocninou smerodajnej odchýlky. Zatiaľ čo rozptyl pomáha kvantifikovať veľkosť variability, smerodajná odchýlka je jednoduchšia na interpretáciu, pretože je vyjadrená v rovnakých jednotkách ako vaše pôvodné dáta. Napríklad, ak meriate hodnotenia spokojnosti, smerodajná odchýlka poskytne intuitívne pochopenie toho, ako sa odpovede líšia od priemeru. Interpretácia výsledkov smerodajnej odchýlky Akonáhle vypočítate smerodajnú odchýlku, môžete ju použiť na interpretáciu konzistentnosti vašich odpovedí v prieskume. Nízka smerodajná odchýlka znamená, že respondenti sú vo všeobecnosti na jednej lodi, kým vysoká smerodajná odchýlka naznačuje rôzne názory. Napríklad, predstavte si, že ste prieskumom skúmali 100 zamestnancov ohľadom ich spokojnosti so zamestnaním na stupnici od 1 do 10. Ak sa väčšina odpovedí sústreďuje okolo 8, s nízkou smerodajnou odchýlkou, naznačuje to všeobecnú spokojnosť. Avšak, ak sa hodnotenia pohybujú od 4 do 10, väčšia smerodajná odchýlka ukazuje, že názory sú viac rozdelené, a možno bude potrebné to podrobnejšie preskúmať. Praktické aplikácie smerodajnej odchýlky Zlepšenie otázok v prieskume: Ak si všimnete vysokú smerodajnú odchýlku pre konkrétnu otázku prieskumu, môže to naznačovať, že otázka je nejednoznačná alebo nie je respondentom dobre pochopená. Vylepšenie formulácie môže pomôcť získať presnejšie údaje v budúcich prieskumoch. Robenie rozhodnutí založených na dátach: Smerodajná odchýlka vám pomáha robiť informovanejšie rozhodnutia tým, že odhaľuje vzory vo vašich prieskumových dátach. Napríklad, ak je spätná väzba veľmi variabilná, môžete segmentovať svoje publikum a prispôsobiť odpovede podľa toho. Zabezpečenie presnosti smerodajnej odchýlky Chýbajúce dáta: Chýbajúce dáta môžu skresliť výpočet smerodajnej odchýlky. Aby ste predišli nepresnostiam, buď zohľadnite chýbajúce dáta vylúčením neúplných odpovedí, alebo použite imputačné techniky. Vyhnutie sa odľahlým hodnotám: Dvojnásobné overenie vašich údajov na chyby alebo odľahlé hodnoty je kľúčové. Aj jedna nesprávna evidencia môže výrazne zmeniť vaše výsledky. Používanie prieskumových nástrojov LimeSurvey môže pomôcť zhromaždiť presné, použiteľné dáta, ktoré odrážajú skutočnú variabilitu. Začatím so pochopením smerodajnej odchýlky odomknete mocné pohľady do vašich výsledkov prieskumu. To vám umožní nielen efektívnejšie interpretovať dáta, ale aj robiť lepšie rozhodnutia na základe hlbšieho pochopenia toho, ako sa cítia, konajú alebo rozmýšľajú vaši respondenti. Po určení smerodajnej odchýlky umožňuje LimeSurvey zlepšiť vaše otázky, takže môžete maximálne využiť váš prieskum a dáta. Vyskúšajte to už dnes!