Tabelleninhalt

Was ist statistische Signifikanz?

Die statistische Signifikanz zeigt an, ob die Ergebnisse einer Umfrage oder eines Experiments wahrscheinlich echt und faktisch sind oder zufällig entstanden sind. Sie hilft Forschern und Unternehmen, die Zuverlässigkeit ihrer Daten zu bestimmen.

Wenn beispielsweise ein Marketingteam herausfindet, dass 55 % der Kunden Limetten-Sorbet gegenüber Ananas bevorzugen, mit einem Signifikanzniveau von 95 %, deutet dies darauf hin, dass die Ergebnisse vertrauenswürdig sind und nicht zufällig zustande kamen.

Warum ist statistische Signifikanz wichtig?

Das Verständnis statistischer Signifikanz ist entscheidend für informierte Entscheidungen. Es hilft Unternehmen, Marketingstrategien zu validieren, Vertrauen und Zuverlässigkeit in die Forschung aufzubauen, datengestützte Entscheidungen zu treffen und Unsicherheiten in Umfrageergebnissen zu reduzieren.

Wie wird statistische Signifikanz berechnet?

Um die statistische Signifikanz Ihrer Daten zu bestimmen, verwenden Sie die folgende Formel:

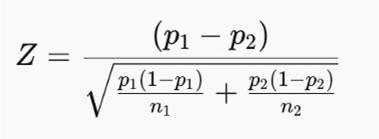
Statistical Significance Calculator

Nun brechen wir diese Variablen auf:

  • p1 und p2 sind die Erfolgsquoten in zwei verschiedenen Gruppen
  • n1 und n2 sind die Stichprobengrößen jeder Gruppe
  • Z misst, wie viele Standardabweichungen der beobachtete Unterschied vom Mittelwert entfernt ist
  • Der p-Wert wird aus Z abgeleitet und bestimmt letztendlich die Signifikanz der Ergebnisse

Der p-Wert wird dann mit einem Signifikanzniveau (typischerweise 0,05 für ein Konfidenzniveau von 95 %) verglichen. Ist der p-Wert niedriger als das Signifikanzniveau, gilt der Unterschied als statistisch signifikant.

Versuchen Sie jetzt unseren Rechner für statistische Signifikanz!

Die Rolle des Konfidenzniveaus bei der statistischen Signifikanz

Bei der Berechnung der statistischen Signifikanz spielen Konfidenzniveaus eine wichtige Rolle: Sie geben die Wahrscheinlichkeit an, dass der beobachtete Effekt real ist. Häufige Konfidenzniveaus sind:

Konfidenzniveau Z-Score
90% 1.64
95% 1.96
99% 2.58

Höhere Konfidenzniveaus bieten stärkere Sicherheit, erfordern jedoch größere Stichproben. Ein Studium mit einem Konfidenzniveau von 90 % kann beispielsweise 500 Teilnehmer erfordern – aber der Forscher müsste 1.000 Teilnehmer befragen, um das Konfidenzniveau auf 99 % zu erhöhen.

Ein Beispiel für die Berechnung der statistischen Signifikanz

Stellen Sie sich vor, Ihr Sorbet-Unternehmen testet zwei verschiedene Landingpage-Designs, um zu bestimmen, welches effektiver ist, um Menschen zur Anmeldung für den Newsletter zu bewegen.

  • Seite A hat eine Konversionsrate von 12 %, was bedeutet, dass von 1.000 Besuchern 120 Personen sich für den Newsletter anmeldeten.
  • Seite B hat eine Konversionsrate von 15 %, was bedeutet, dass von 1.000 Besuchern 150 Personen dieselbe Aktion durchführten.

Auf den ersten Blick scheint Seite B besser abzuschneiden – doch ist dieser Unterschied zufällig oder statistisch signifikant?

Um dies zu beantworten, muss das Unternehmen die statistische Signifikanz berechnen.

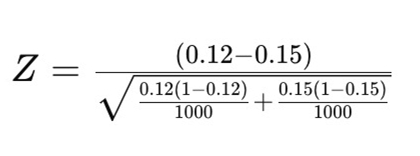
Beispiel für die Berechnung der statistischen Signifikanz

Sobald das Team den p-Wert kennt, kann es diesen mit dem gewählten Konfidenzniveau vergleichen. Möchte man ein Konfidenzniveau von 95 %, muss der p-Wert unter 0,05 liegen, um statistisch signifikant zu sein. Das bedeutet, dass die Verbesserung der Konversionen wahrscheinlich real und nicht zufällige Variation ist.

Wenn der p-Wert jedoch größer als 0,05 ist, könnte der beobachtete Unterschied zufällig sein, und es könnte weitere Tests mit einer größeren Stichprobe erforderlich sein, um das Ergebnis zu bestätigen.

Durch Tests zur statistischen Signifikanz kann das Unternehmen mit Zuversicht die besser funktionierende Seite wählen, um Newsletter-Anmeldungen zu optimieren.

Wie die statistische Signifikanz Umfrageergebnisse beeinflusst

Umfrageergebnisse, die statistische Signifikanz erreichen, weisen auf signifikante Unterschiede zwischen den Befragten hin und helfen Forschern und Unternehmen, die Validität ihrer Daten zu bestätigen und größeres Vertrauen zu gewinnen. Dies ist nützlich für:

Wie die statistische Signifikanz verbessert werden kann

Ein höherer statistischer Signifikanzwert verringert die Wahrscheinlichkeit, dass Ergebnisse zufällig sind, was die Forschung glaubwürdiger und wirkungsvoller macht. Falls ein statistischer Signifikanzwert erhöht werden muss, um die Zuverlässigkeit der Ergebnisse zu steigern oder sicherzustellen, dass datengestützte Entscheidungen auf bedeutungsvollen Ergebnissen basieren, gibt es verschiedene Möglichkeiten, den nächsten Test zu gestalten.

Statistische Signifikanzwerte können verbessert werden durch:

  • Erhöhung der Stichprobengröße
  • Reduktion der Variabilität in der Datenerhebung
  • Nutzung eines höheren Konfidenzniveaus für stärkere Zuverlässigkeit
  • Formulierung klarer und unvoreingenommener Fragen während des Umfrageerstellungsprozesses

Statistische Signifikanz ist ein entscheidender Faktor, um zu bestimmen, ob Umfrageergebnisse zuverlässig sind. Mit der richtigen Methodik und Stichprobengröße können Unternehmen und Forscher mit Zuversicht datengestützte Entscheidungen treffen.

Versuchen Sie noch heute unseren kostenlosen Rechner für statistische Signifikanz, um Ihre Ergebnisse zu validieren!

Jetzt berechnen

Erstelle jetzt deine erste Umfrage!
So einfach wie eine Limette auszupressen.

Registrieren

  • Erstelle Umfragen in über 40 Sprachen
  • Unbegrenzte Anzahl von Nutzern
  • Sofort einsatzbereite Umfragevorlagen
  • Und vieles mehr...