Tabelleninhalt

Was ist statistische Signifikanz?

Statistische Signifikanz zeigt, ob die Ergebnisse einer Umfrage oder eines Experiments wahrscheinlich echt und zuverlässig sind – und nicht zufällig entstanden. Sie hilft Forschenden und Unternehmen, die Verlässlichkeit ihrer Daten zu beurteilen.

Wenn zum Beispiel ein Marketingteam herausfindet, dass 55 % der Kundschaft Sorbet mit Limettengeschmack gegenüber Ananas bevorzugen – bei einem Signifikanzniveau von 95 % –, deutet dies darauf hin, dass die Ergebnisse vertrauenswürdig sind und nicht zufällig entstanden.

Warum ist statistische Signifikanz wichtig?

Das Verständnis von statistischer Signifikanz ist entscheidend für fundierte Entscheidungen. Sie hilft Unternehmen, Marketingstrategien zu validieren, Vertrauen und Zuverlässigkeit in der Forschung aufzubauen, datenbasierte Entscheidungen zu treffen und die Unsicherheit in Umfrageergebnissen zu verringern.

Wie wird statistische Signifikanz berechnet?

Um die statistische Signifikanz Ihrer Daten zu bestimmen, verwenden Sie die folgende Formel:

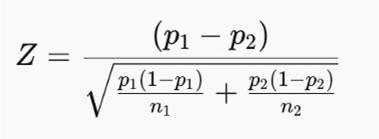
Statistical Significance Calculator

Die Variablen bedeuten:

  • p1 und p2 = die Erfolgsanteile in zwei verschiedenen Gruppen
  • n1 und n2 = die Stichprobengrössen jeder Gruppe
  • Z = misst, wie viele Standardabweichungen die beobachtete Differenz vom Mittelwert entfernt ist
  • Der Wert p wird aus Z abgeleitet und bestimmt letztlich die Signifikanz der Ergebnisse

Der p-Wert wird mit einem Signifikanzniveau verglichen (typischerweise 0.05 für ein Konfidenzniveau von 95 %). Ist der p-Wert kleiner, gilt der Unterschied als statistisch signifikant.

Jetzt unseren Signifikanz-Rechner ausprobieren!

Die Rolle von Konfidenzniveaus bei der statistischen Signifikanz

Beim Berechnen der statistischen Signifikanz spielen Konfidenzniveaus eine zentrale Rolle: Sie geben die Wahrscheinlichkeit an, dass der beobachtete Effekt real ist. Gängige Konfidenzniveaus sind:

Konfidenzniveau Z-Wert
90 % 1.64
95 % 1.96
99 % 2.58

Höhere Konfidenzniveaus bieten stärkere Sicherheit, erfordern aber grössere Stichproben. Ein Beispiel: Bei 90 % Konfidenz braucht eine Studie vielleicht 500 Teilnehmende – für 99 % Konfidenz könnten es 1’000 sein.

Beispiel zur Berechnung statistischer Signifikanz

Stellen Sie sich vor, Ihr Sorbet-Unternehmen testet zwei verschiedene Landingpages, um herauszufinden, welche mehr Newsletter-Anmeldungen bringt.

  • Seite A: 12 % Conversion Rate → von 1’000 Besuchenden haben sich 120 angemeldet.
  • Seite B: 15 % Conversion Rate → von 1’000 Besuchenden haben sich 150 angemeldet.

Auf den ersten Blick scheint Seite B besser zu sein – aber ist der Unterschied zufällig oder statistisch signifikant?

Um das herauszufinden, muss die statistische Signifikanz berechnet werden.

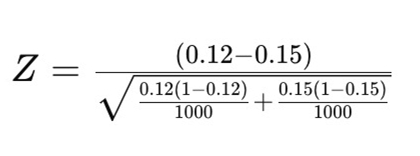
Beispiel zur Berechnung der statistischen Signifikanz

Hat das Team den p-Wert, kann es diesen mit dem gewünschten Konfidenzniveau vergleichen. Bei 95 % Konfidenz muss der p-Wert kleiner als 0.05 sein, um statistisch signifikant zu sein. Das bedeutet, dass die Verbesserung bei den Conversions wahrscheinlich real ist und nicht auf Zufall beruht.

Ist der p-Wert hingegen grösser als 0.05, könnte der Unterschied zufällig sein – dann ist eine grössere Stichprobe nötig, um das Ergebnis zu bestätigen.

Mit statistischer Signifikanzprüfung kann das Unternehmen sicher die bessere Seite wählen und die Newsletter-Anmeldungen optimieren.

Wie statistische Signifikanz Umfrageergebnisse beeinflusst

Umfrageergebnisse mit statistischer Signifikanz zeigen echte Unterschiede zwischen den Befragten und helfen Forschenden sowie Unternehmen, die Gültigkeit ihrer Daten zu bestätigen und Vertrauen aufzubauen. Nützlich ist dies zum Beispiel für:

Wie lässt sich statistische Signifikanz verbessern?

Ein höheres Signifikanzniveau verringert die Wahrscheinlichkeit, dass Ergebnisse zufällig sind, und macht Studien aussagekräftiger. Wenn die Signifikanz verbessert werden soll – etwa um die Verlässlichkeit zu erhöhen oder sicherzustellen, dass datenbasierte Entscheidungen auf relevanten Ergebnissen beruhen –, gibt es verschiedene Ansätze:

  • Erhöhung der Stichprobengrösse
  • Reduzierung der Variabilität bei der Datenerhebung
  • Verwendung eines höheren Konfidenzniveaus für stärkere Zuverlässigkeit
  • Klare und neutrale Fragestellung in der Umfrage

Statistische Signifikanz ist ein zentraler Faktor, um die Verlässlichkeit von Umfrageergebnissen zu bestimmen. Mit der richtigen Methodik und Stichprobengrösse können Unternehmen und Forschende sicher datenbasierte Entscheidungen treffen.

Probieren Sie unseren kostenlosen Signifikanz-Rechner aus und validieren Sie Ihre Ergebnisse!

Jetzt berechnen

Erstellen Sie jetzt Ihre erste Umfrage!
So einfach wie ein Spritzer Limette.

Jetzt registrieren

  • Umfragen in über 40 Sprachen erstellen
  • Unbegrenzte Anzahl an Nutzern
  • Sofort einsatzbereite Umfragevorlagen
  • Und vieles mehr …