Contenido de la tabla
¿Qué es la Significancia Estadística?
La significancia estadística indica si los resultados de una encuesta o experimento son genuinos y verídicos, en lugar de ocurrir por casualidad. Ayuda a investigadores y empresas a determinar la fiabilidad de sus datos.
Por ejemplo, si un equipo de marketing encuentra que el 55% de los clientes prefieren el sorbete de lima frente al de piña con un nivel de significancia del 95%, sugiere que los resultados son confiables y no se deben al azar.
¿Por Qué es Importante la Significancia Estadística?
Entender la significancia estadística es crucial para tomar decisiones informadas. Ayuda a las empresas a validar estrategias de marketing, construir confianza y fiabilidad en la investigación, tomar decisiones basadas en datos y reducir la incertidumbre en los resultados de encuestas.
¿Cómo se Calcula la Significancia Estadística?
Para determinar la significancia estadística de tus datos, utiliza la siguiente fórmula:
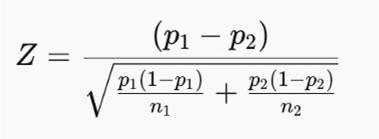
Ahora, desglosamos estas variables:
- p1 y p2 son las proporciones de éxito en dos grupos diferentes
- n1 y n2 son los tamaños de muestra de cada grupo
- Z mide cuántas desviaciones estándar está la diferencia observada de la media
- El valor de p se deriva de Z y determina la significancia de los resultados
El valor p se compara con un nivel de significancia (típicamente 0.05 para un nivel de confianza del 95%). Si el valor p es inferior al nivel de significancia, la diferencia se considera estadísticamente significativa.
¡Prueba nuestra calculadora de significancia estadística ahora!
El Rol de los Niveles de Confianza en la Significancia Estadística
Al calcular la significancia estadística, los niveles de confianza juegan un papel importante: indican la probabilidad de que el efecto observado sea real. Los niveles de confianza comunes incluyen:
| nivel de confianza | puntuación Z |
|---|---|
| 90% | 1.64 |
| 95% | 1.96 |
| 99% | 2.58 |
Niveles de confianza más altos proporcionan mayor certeza, pero requieren muestras más grandes. Por ejemplo, un estudio realizado con un nivel de confianza del 90% puede requerir 500 participantes, pero el investigador necesitará encuestar a 1,000 participantes para aumentar el nivel de confianza al 99%.
Un Ejemplo de Cálculo de Significancia Estadística
Imagina que tu empresa de sorbetes está probando dos diseños diferentes de página de destino para determinar cuál es más efectivo para que las personas se inscriban en tu boletín.
- La Página A tiene una tasa de conversión del 12%, lo que significa que de 1,000 visitantes, 120 personas se inscribieron en el boletín.
- La Página B tiene una tasa de conversión del 15%, lo que significa que de 1,000 visitantes, 150 personas completaron la misma acción.
A primera vista, la Página B parece estar rindiendo mejor, pero ¿es esta diferencia debido al azar, o es estadísticamente significativa?
Para responder a esto, la empresa necesita calcular la significancia estadística.
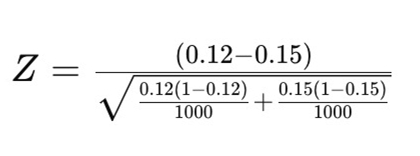
Una vez que el equipo conoce el valor p, puede compararlo con su nivel de confianza deseado. Si quieren un nivel de confianza del 95%, el valor p debe ser menor a 0.05 para que sea estadísticamente significativo. Esto significa que la mejora en las conversiones es probable que sea real y no variación aleatoria.
Sin embargo, si el valor p es mayor a 0.05, la diferencia observada podría deberse al azar, y se necesitará más pruebas con una muestra más grande para confirmar el resultado.
Con la prueba de significancia estadística, la empresa puede elegir con confianza la página que mejor rinde para optimizar las inscripciones al boletín.
Cómo la Significancia Estadística Afecta los Resultados de Encuestas
Los resultados de encuestas que logran significancia estadística indican diferencias significativas entre los encuestados, ayudando a investigadores y empresas a confirmar la validez de sus datos mientras generan mayor confianza. Esto es útil para:
- Pruebas A/B en marketing
- Encuestas de satisfacción del cliente
- Encuestas electorales
- Estudios de preferencias de productos
Cómo Mejorar la Significancia Estadística
Un puntaje de significancia estadística más alto reduce la probabilidad de que los resultados se deban al azar, haciendo que la investigación sea más creíble y relevante. En caso de que se necesite mejorar un puntaje de significancia estadística, ya sea para aumentar la fiabilidad de los hallazgos o para asegurar que las decisiones basadas en datos sean significativas, hay varias maneras de diseñar la próxima prueba.
Los puntajes de significancia estadística se pueden mejorar mediante:
- Aumentar el tamaño de la muestra
- Reducir la variabilidad en la recolección de datos
- Usar un nivel de confianza más alto para mayor fiabilidad
- Formular preguntas claras y imparciales durante el proceso de creación de encuestas
La significancia estadística es un factor clave para determinar si los resultados de la encuesta son confiables. Con la metodología y el tamaño de muestra adecuados, las empresas e investigadores pueden tomar decisiones basadas en datos con confianza.
¡Prueba nuestra Calculadora de Significancia Estadística gratuita hoy para validar tus hallazgos!
¡Crea tu primera encuesta ahora!
Es tan fácil como exprimir una lima.
- Crea encuestas en más de 40 idiomas
- Número ilimitado de usuarios
- Más de 800 plantillas de encuestas listas para usar
- Y mucho más...