Tabelleninhalt
Was ist die Fehlermarge?
Die Fehlermarge ist eine Statistik, die die Unsicherheit in Ihren Umfrageergebnissen quantifiziert.
Eine kleinere Fehlermarge zeigt an, dass Ihre Umfrageergebnisse mit grösserer Wahrscheinlichkeit genau sind, während eine grössere Fehlermarge auf eine höhere Unsicherheit und eine breitere Spannweite möglicher Ergebnisse hinweist. Die akzeptable Fehlermarge liegt bei einem Konfidenzniveau von 95 % zwischen 4 % und 8 %.
Warum ist die Fehlermarge wichtig?
Eine gut berechnete Fehlermarge stellt sicher, dass Ihre Umfrageergebnisse vertrauenswürdig sind, die Gesamtbevölkerung widerspiegeln und die Unsicherheit in Ihren Erkenntnissen ehrlich darstellen – all dies ist entscheidend, um Glaubwürdigkeit zu bewahren und fundierte Entscheidungen zu treffen.
Wie wird die Fehlermarge berechnet?
Um die Fehlermarge zu berechnen, müssen Sie Ihre Stichprobengrösse (𝑛), den Z-Wert (𝑍) und die Standardabweichung (𝜎) kennen.
Der Z-Wert entspricht dem gewünschten Konfidenzniveau und zeigt an, wie weit ein Datenpunkt in Standardabweichungseinheiten vom Mittelwert entfernt ist. Zum Vergleich: Ein Konfidenzniveau von 95 % ist mit einem Z-Wert von 1.96 verbunden, während ein Konfidenzniveau von 99 % einem Z-Wert von 2.58 entspricht.
Als Nächstes müssen Sie die Standardabweichung bestimmen, die die Streuung Ihrer Daten misst. Wenn Sie mit Anteilen arbeiten (z. B. dem Prozentsatz der Befragten, die eine bestimmte Option gewählt haben), verwenden Sie diesen Anteil anstelle der Standardabweichung.
Sobald Sie den Z-Wert und die Standardabweichung kennen, können Sie die Fehlermarge mit folgender Formel berechnen:
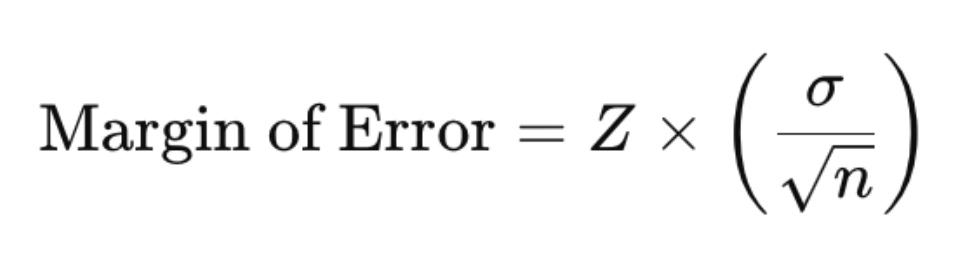
Die Formel verdeutlicht die umgekehrte Beziehung zwischen Stichprobengrösse und Fehlermarge: Mit zunehmender Stichprobengrösse sinkt die Fehlermarge.
Die Rolle des Konfidenzintervalls bei der Fehlermarge
Wie oben gezeigt, ist das Konfidenzintervall ein Schlüsselelement bei der Berechnung der Fehlermarge. Es gibt den Bereich an, in dem der wahre Bevölkerungswert voraussichtlich liegt. Ein 95 %-Konfidenzintervall bedeutet beispielsweise, dass Sie zu 95 % sicher sein können, dass der wahre Wert innerhalb dieses Bereichs liegt. Dies erhöht die Genauigkeit und Zuverlässigkeit der Stichprobenergebnisse.
Wie Stichprobengrösse und Standardabweichung die Fehlermarge beeinflussen
Die beiden weiteren Hauptfaktoren bei der Bestimmung der Fehlermarge sind die Stichprobengrösse und die Standardabweichung der Daten.
- Stichprobengrösse: Generell gilt: Je grösser Ihre Stichprobe, desto kleiner die Fehlermarge. Eine grössere Stichprobe repräsentiert die tatsächliche Bevölkerung zuverlässiger.
Standardabweichung: Die Standardabweichung misst die Streuung der Daten. Bei hoher Standardabweichung (die Daten sind stark gestreut) ist die Fehlermarge grösser. Eine niedrige Standardabweichung (die Daten sind eng beieinander) bedeutet eine kleinere Fehlermarge. Weniger Variation in den Daten führt also zu zuverlässigeren Ergebnissen.
Beispiel zur Berechnung der Fehlermarge
Nehmen wir an, Sie sind ein Unternehmen, das auf Glacés spezialisiert ist, und möchten die Kundenzufriedenheit mit Ihrem neuen Limettengeschmack messen. Sie befragen 400 Personen und stellen fest, dass 50 % mit Ihrem Produkt zufrieden sind. Mit einer Standardabweichung von 0.5 und einem Konfidenzniveau von 95 % würde die Fehlermarge wie folgt berechnet:
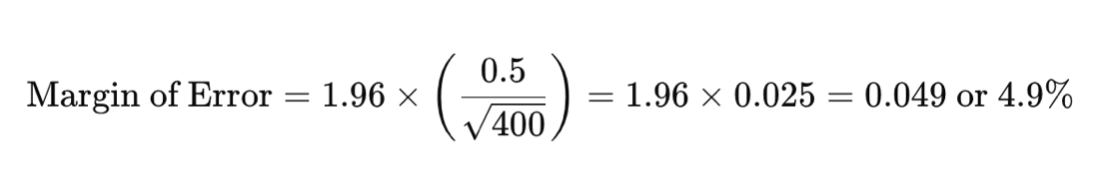
Das bedeutet, dass der tatsächliche Prozentsatz der Bevölkerung, die zufrieden ist, wahrscheinlich zwischen 45.1 % und 54.9 % liegt.
Zwei Stichproben vergleichen: Welche Rolle spielt die Fehlermarge?
In manchen Fällen möchten Sie zwei verschiedene Gruppen oder Stichproben vergleichen. Zum Beispiel wollen Sie die Lieblingsgeschmacksrichtungen von Glacé bei Kindern und Erwachsenen ermitteln. Wenn beide Gruppen gross sind und kleine Fehlermargen haben, lassen sich die Ergebnisse leichter sinnvoll vergleichen.
Wenn jedoch eine Gruppe eine sehr grosse und die andere eine kleine Fehlermarge hat, wird es schwieriger, aus dem Vergleich Schlussfolgerungen zu ziehen. Die grössere Fehlermarge könnte bedeuten, dass der Unterschied zwischen den Gruppen weniger signifikant ist, als es zunächst scheint. Überschneiden sich die Intervalle, sind die Unterschiede möglicherweise gar nicht statistisch signifikant. Diese Feinheiten können beim Interpretieren von Umfrageergebnissen entscheidend sein und zeigen, warum es wichtig ist, die Fehlermarge beim Vergleich verschiedener Gruppen zu berücksichtigen.
Das Zusammenspiel von Punktschätzung und Fehlermarge
In der Statistik ist eine Punktschätzung ein einzelner Wert, der als Schätzung für einen Parameter der Grundgesamtheit dient (z. B. der Prozentsatz der Personen, die Limette gegenüber Kirsche bevorzugen). Es ist ein bisschen wie ein Dartpfeilwurf: Sie hoffen, das Bullseye zu treffen – die Fehlermarge zeigt Ihnen, wie nah Sie wahrscheinlich dran sind.
Anders gesagt: Die Fehlermarge liefert einen Bereich, in dem der wahre Wert der Punktschätzung wahrscheinlich liegt. Wenn Ihre Punktschätzung beispielsweise 60 % beträgt und die Fehlermarge ±3 % ist, liegt der wahre Bevölkerungswert zwischen 57 % und 63 %.
Zusammen liefern diese beiden Kennzahlen ein klareres Bild, anstatt sich nur auf eine einzige Zahl zu verlassen.
Wie die Fehlermarge Umfrageergebnisse beeinflusst
Bei der Nutzung von Umfragedaten ist die Fehlermarge oft ein zentraler Bestandteil, um die Ergebnisse verständlich darzustellen.
Eine kleine Fehlermarge bedeutet mehr Präzision und Vertrauen in die Ergebnisse, während eine grosse Fehlermarge auf mehr Unsicherheit hinweist. Wenn beispielsweise eine Umfrage zeigt, dass Kirsche mit 3 % Vorsprung als Lieblingsgeschmack führt, die Fehlermarge aber ±5 % beträgt, könnte der Vorsprung in Wirklichkeit 2 % Rückstand oder 8 % Vorsprung bedeuten. Das ist eine grosse Spanne, die die Ergebnisse weniger eindeutig macht.
Die Fehlermarge ist ein wesentliches Element, das zeigt, wie viel Vertrauen man in die Resultate setzen kann. Je kleiner die Marge, desto wahrscheinlicher spiegeln die Ergebnisse der Stichprobe die Realität wider.
Wie sich die Fehlermarge verringern lässt
Wenn Sie die Stichprobengrösse erhöhen oder die Standardabweichung verringern, reduziert sich die Fehlermarge. Ihre Schätzung liegt dann näher am wahren Bevölkerungswert.
Wenn Ihre Fehlermarge bei einem bestimmten Konfidenzniveau zu hoch ist, sollten Sie die Stichprobengrösse erhöhen. Je mehr Daten Sie erheben, desto näher kommen Ihre Ergebnisse dem wahren Wert.
In der Welt von Umfragen, Befragungen und Statistiken ist die Fehlermarge ein unverzichtbares Werkzeug, um sicherzustellen, dass die Zahlen nicht irreführend sind, indem sie einen Grad an Sicherheit in die Daten bringt.
Das nächste Mal, wenn Sie ein Umfrageergebnis mit einer Fehlermarge sehen, denken Sie daran, was diese Zahl wirklich bedeutet. Es ist nicht nur eine Statistik, sondern ein Hinweis darauf, wie zuverlässig die Daten sind – und wie viel Spielraum für Fehler besteht.
Desto kleiner die Fehlermarge, desto grösser Ihr Vertrauen in die Ergebnisse. Also, worauf warten Sie? Berechnen Sie jetzt Ihre Fehlermarge und arbeiten Sie daran, die Unsicherheit zu verringern!
Erstellen Sie jetzt Ihre erste Umfrage!
So einfach wie ein Spritzer Limette.
- Umfragen in über 40 Sprachen erstellen
- Unbegrenzte Anzahl an Nutzern
- Sofort einsatzbereite Umfragevorlagen
- Und vieles mehr …