Taulukon sisältö
Mikä on virhemarginaali?
Virhemarginaali on tilastotieto, joka kvantifioi epävarmuuden kyselytutkimustesi tuloksissa.
Pienempi virhemarginaali tarkoittaa, että tutkimustuloksesi todennäköisesti ovat tarkempia, kun taas suurempi virhemarginaali viittaa suurempaan epävarmuuteen ja laajempaan mahdollisten tulosten joukkoon. Hyväksyttävä virhemarginaali on 4%–8% 95% luottamustasolla.
Waarom virhemarginaali on tärkeä?
Hyvin laskettu virhemarginaali varmistaa, että kyselytutkimustesi tulokset ovat luotettavia, heijastavat laajempaa väestöä ja ovat rehellisiä mahdolisesta epävarmuudesta—all of which are vital for maintaining credibility and making informed decisions.
Kuinka virhemarginaali lasketaan?
Virhemarginaalin laskemiseksi tarvitset tiedot otoskooltasi (𝑛), Z-pisteestä (𝑍) ja keskihajonnasta (𝜎).
Z-pisteen määrittäminen: Z-piste vastaa haluttua luottamustasoa, mikä tarkoittaa, kuinka kaukana datapiste on keskiarvosta keskihajontayksiköissä. Esimerkiksi 95% luottamustaso liittyy Z-pisteeseen 1.96 ja 99% luottamustaso Z-pisteeseen 2.58.
Seuraavaksi sinun on määritettävä keskihajonta, joka mittaa tietojen vaihtelua. Jos käsittelet suhteita (esim. prosenttia vastaajista, jotka valitsivat tietyn vaihtoehdon), käytät suhteellista arvoa keskihajonnan sijaan.
Kun tiedät Z-pisteen ja keskihajonnan, voit laskea virhemarginaalin seuraavalla kaavalla:
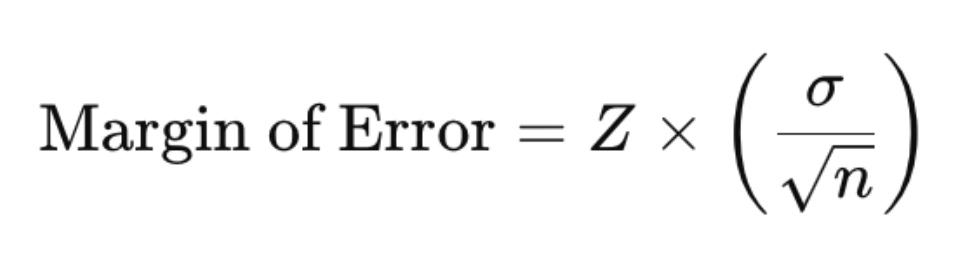
Kaava korostaa käänteistä suhdetta otoskoon ja virhemarginaalin välillä: kun otoskoko kasvaa, virhemarginaali pienenee.
Luottamusvälin rooli virhemarginaalissa
Kuten edellä on osoitettu, luottamusväli on avainkomponentti virhemarginaalin laskemisessa, joka antaa alueen, johon todellinen väestöarvo todennäköisesti kuuluu. Esimerkiksi 95% luottamusväli tarkoittaa, että olet 95% varma siitä, että todellinen arvo on tuolla alueella. Tämä tuo tarkkuutta ja parantaa otoksen tulosten luotettavuutta ja tarkkuutta.
Kuinka otoskoko ja keskihajonta vaikuttavat virhemarginaaliin
Kaksi päätekijää virhemarginaalin määrittämisessä ovat otoskoko ja tietojen keskihajonta.
- Otoskoko: Yleisesti ottaen mitä suurempi otoskoko, sitä pienempi virhemarginaali. Suurempi otos todennäköisemmin edustaa todellista väestöä.
Keskihajonta: Keskihajonta mittaa tietojen hajontaa tai vaihtelua. Jos datallasi on korkea keskihajonta (eli se on hyvin hajautettu), virhemarginaali on suurempi. Alhainen keskihajonta (tiivis data) tarkoittaa pienempää virhemarginaalia. Yhteenvetona: vähemmän vaihtelua datassa johtaa luotettavampiin tuloksiin.
Virhemarginaalin lask esimerkki
Oletetaan, että olet yritys, joka erikoistuu jäätelöön, ja haluat saada tietoa asiakkaiden tyytyväisyydestä uuteen lime-makuusi. Kysyt 400 ihmiseltä ja huomaat, että 50% heistä on tyytyväisiä jäädykkeeseesi. Käytetään keskihajontaa 0.5 ja 95% luottamustasoa, virhemarginaali lasketaan seuraavasti:
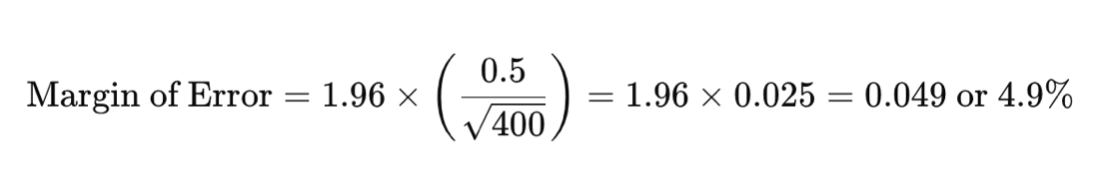
Tämä tarkoittaa, että todellinen prosentti väestöstä, joka on tyytyväinen asiakaskokemukseen, on todennäköisesti välillä 45.1% ja 54.9%.
Kaksi otosta vertailtaessa: Miten virhemarginaali vaikuttaa?
Joissakin tapauksissa saatat haluta vertailla kahta eri ryhmää tai otosta. Esimerkiksi toivot kerääväsi tietoa lasten ja aikuisten suosikkijäätelömaista. Jos molemmat ryhmät ovat suuria ja niiden virhemarginaalit pieniä, on helpompaa tehdä merkityksellinen vertailu.
Kuitenkin, jos toisella ryhmällä on erittäin suuri virhemarginaali ja toisella pieni, vertailusta johtuvien johtopäätösten tekeminen on haastavampaa. Suurempi virhemarginaali voisi tarkoittaa, että ero ryhmien välillä ei ole niin merkittävä kuin se aluksi vaikuttaa. Jos välin yli menee, eroja ei ehkä ole tilastollisesti merkittäviä. Tämä nyanssi voi vaikuttaa suuresti kyselytutkimustulosten tulkintaan ja korostaa virhemarginaalin tarkistamisen tärkeyttä eri ryhmien tuloksia verrattaessa.
Pistetiarvon ja virhemarginaalin suhteen ymmärtäminen
Tilastoissa pistetiarvo on yksittäinen arvo, jota käytetään väestöparametrin (kuten prosenttina ihmisistä, jotka suosivat lime-maustettuja jäätelöitä kirsikka-maustettujen yli) arvioimiseen. Se on kuin heittäisi nuolta tarkkuuslaukauspelissä ja toivoo osuvansa tauluun—mutta virhemarginaali kertoo, kuinka lähellä se nuoli saattaa olla osumasta.
Toisin sanoen, virhemarginaali antaa meille alueen, jossa todennäköisesti löydämme oikean arvon pistetiarvolle, näyttäen mahdolliset arvot. Joten, jos pistetiarvo on 60% ja virhemarginaali on ±3%, todellinen väestöp prosentti voisi olla missä tahansa 57%:sta 63%:iin.
Nämä kaksi tilastoa tarjoavat yhdessä selvemmän kuvan siitä, mitä todella tarkastellaan, sen sijaan että luotettaisiin vain yhteen lukuun.
Kuinka virhemarginaali vaikuttaa kyselytutkimustuloksiin
Kyselytutkimustiedon käyttämisessä virhemarginaali on usein avainkomponentti, joka auttaa yleisöä ymmärtämään tulokset paremmin.
Pieni virhemarginaali viittaa tarkkuuteen ja luottamukseen kyselytutkimustuloksissa, kun taas suurempi virhemarginaali tarkoittaa suurempaa epävarmuutta. Esimerkiksi tutkimus, joka osoittaa kirsikan olevan suosikkimaku 3% erolla virhemarginaalilla ±5%, tarkoittaa, että etumatka voisi olla jopa 2% jäljessä tai jopa 8% edellä. Tämä on melko suuri vaihtelu, mikä tekee tuloksista vähemmän ratkaisevia.
Virhemarginaali on olennainen osa kuvaa, joka auttaa ihmisiä ymmärtämään, kuinka paljon luottamusta he voivat antaa kysely- tai tutkimustuloksille. Mitä pienempi marginaali, sitä todennäköisemmin otoksen tulokset heijastavat väestön todellista kuvaa.
Kuinka vähentää virhemarginaalia
Kun kasvatat otoskokoasi tai pienennät keskihajontaa, tiivistät virhemarginaaliasi, mikä tarkoittaa, että arviosi on todennäköisemmin lähellä todellista väestöarvoa.
Jos huomaat, että virhemarginaalisi on liian korkea halutun luottamustason perusteella, on ratkaisevan tärkeää kasvattaa otoskokoasi. Mitä enemmän tietoa keräät, sitä lähempänä tuloksesi ovat todellista väestöarvoa.
Kyselytutkimusten, äänestysten ja tilastojen maailmassa virhemarginaali on tärkeä työkalu, joka varmistaa, etteivät luvut ole harhaanjohtavia tarjoamalla varmuudenaste datalle.
Kun seuraavan kerran näet kyselytutkimustuloksen virhemarginaalilla, käytä hetki miettiäksesi, mitä tuo luku todella tarkoittaa. Se ei ole vain tilasto; se on merkki siitä, kuinka luotettavaa data on—ja kuinka paljon virhemarginaalille voi olla tilaa.
Muista, mitä pienempi virhemarginaali, sitä varmempi voit olla johtopäätöksissäsi. Joten, mitä odotat? Lasketaan virhemarginaalisi ja ryhdytään tekemään työtä epävarmuuden vähentämiseksi!
Luo ensimmäinen kyselysi nyt!
Se on yhtä helppoa kuin limen puristaminen.
- Luo kyselyjä yli 40 kielellä
- Rajaton määrä käyttäjiä
- Yli 800 valmista kyselymallia
- Paljon muuta...