เนื้อหาตาราง
ข้อผิดพลาดของขอบเขตคืออะไร?
ข้อผิดพลาดของขอบเขต คือสถิติที่วัดความไม่แน่นอนในผลการสำรวจของคุณ
ข้อผิดพลาดของขอบเขตที่เล็กลงหมายความว่าผลการสำรวจมีความแม่นยำมากขึ้น ในขณะที่ข้อผิดพลาดที่มากขึ้นแสดงถึงความไม่แน่นอนมากขึ้นและช่วงที่กว้างขึ้นของผลลัพธ์ที่เป็นไปได้ ข้อผิดพลาดที่ยอมรับได้จะอยู่ระหว่าง 4% ถึง 8% ในระดับความเชื่อมั่น 95%
ทำไมข้อผิดพลาดของขอบเขตถึงสำคัญ?
ข้อผิดพลาดที่คำนวณได้อย่างถูกต้องทำให้ผลการสำรวจของคุณเชื่อถือได้ สะท้อนประชากรในวงกว้าง และตรงไปตรงมาถึงความไม่แน่นอนในผลลัพธ์ ซึ่งทั้งหมดนี้มีความสำคัญต่อการรักษาความน่าเชื่อถือและการตัดสินใจอย่างมีข้อมูล
วิธีการคำนวณข้อผิดพลาดของขอบเขต?
ในการคำนวณข้อผิดพลาดของขอบเขต คุณต้องรู้ขนาดตัวอย่าง (𝑛), Z-score (𝑍) และค่าเบี่ยงเบนมาตรฐาน (𝜎)
เพื่อหาค่า Z-score ซึ่งสัมพันธ์กับระดับความเชื่อมั่นที่ต้องการ ตัวอย่างเช่นระดับความเชื่อมั่น 95% จะมี Z-score เท่ากับ 1.96
จากนั้นต้องหาค่าเบี่ยงเบนมาตรฐาน ซึ่งเป็นการวัดความแตกต่างในข้อมูล ถ้าคุณจัดการกับสัดส่วน (เช่น เปอร์เซ็นต์ของผู้ตอบที่เลือกตัวเลือกเฉพาะ) คุณจะใช้สัดส่วนแทนค่าเบี่ยงเบนมาตรฐาน
เมื่อคุณทราบค่า Z-score และค่าเบี่ยงเบนมาตรฐานแล้ว คุณสามารถคำนวณข้อผิดพลาดของขอบเขตได้ตามสูตรนี้:
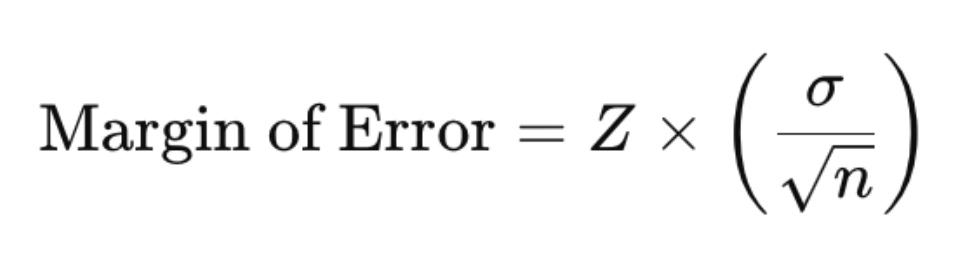
สูตรแสดงให้เห็นถึงความสัมพันธ์ผกผันระหว่างขนาดตัวอย่างและข้อผิดพลาดของขอบเขต: เมื่อขนาดตัวอย่างเพิ่มขึ้น ข้อผิดพลาดของขอบเขตจะลดลง
บทบาทของช่วงความเชื่อมั่นในข้อผิดพลาดของขอบเขต
อย่างที่แสดงให้เห็น ขอบเขตความเชื่อมั่นเป็นส่วนสำคัญเมื่อคำนวณข้อผิดพลาดของขอบเขต โดยให้ช่วงค่าที่คาดว่าจะเป็นค่าของประชากร หากช่วงความเชื่อมั่นอยู่ที่ 95% หมายความว่าคุณมั่นใจ 95% ว่าค่าจริงอยู่ในช่วงนั้น
ขนาดตัวอย่างและค่าเบี่ยงเบนมาตรฐานมีผลต่อข้อผิดพลาดของขอบเขตอย่างไร
ปัจจัยหลักอีกสองประการในการกำหนดข้อผิดพลาดของขอบเขตคือขนาดตัวอย่างและค่าเบี่ยงเบนมาตรฐานของข้อมูล
- ขนาดตัวอย่าง: โดยทั่วไปขนาดตัวอย่างที่ใหญ่กว่าจะมีข้อผิดพลาดของขอบเขตที่เล็กลง เพราะขนาดตัวอย่างที่ใหญ่กว่าจะมีโอกาสแสดงประชากรที่แท้จริงมากขึ้น
ค่าเบี่ยงเบนมาตรฐาน: วัดความกระจายหรือความเปลี่ยนแปลงของข้อมูล หากค่ามีค่าเบี่ยงเบนมาตรฐานสูง (ข้อมูลที่กระจายออกไปมาก) ข้อผิดพลาดจะมากขึ้น และถ้าเบี่ยงเบนมาตรฐานต่ำ (ข้อมูลที่รวมกลุ่มกันแน่น) จะทำให้ข้อผิดพลาดเล็กลง
ตัวอย่างการคำนวณข้อผิดพลาดของขอบเขต
สมมติว่าคุณเป็นบริษัทที่เชี่ยวชาญด้านน้ำแข็งหลอด และต้องการทราบความพึงพอใจของลูกค้าเกี่ยวกับรสชาติใหม่ของมะนาว คุณได้สำรวจผู้คน 400 คนและพบว่ามีผู้ตอบ 50% ที่พอใจกับขนมแช่แข็งของคุณ โดยมีค่าเบี่ยงเบนมาตรฐาน 0.5 และระดับความเชื่อมั่น 95% ข้อผิดพลาดของขอบเขตจะคำนวณได้ดังนี้:
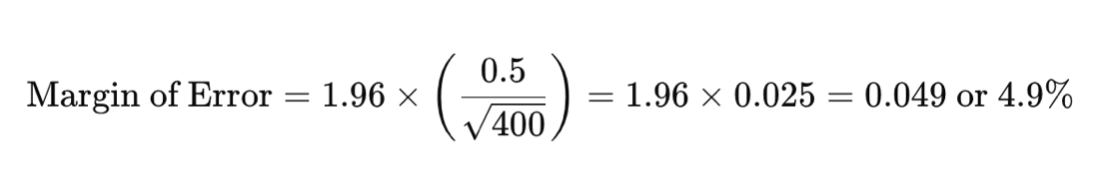
ซึ่งหมายความว่าเปอร์เซ็นต์ที่แท้จริงของประชากรที่มีความสุขกับประสบการณ์ของลูกค้าน่าจะอยู่ระหว่าง 45.1% ถึง 54.9%
การเปรียบเทียบสองตัวอย่าง: ข้อผิดพลาดของขอบเขตมีผลอย่างไร?
ในบางกรณี คุณอาจต้องการเปรียบเทียบสองกลุ่มหรือสองตัวอย่าง ตัวอย่างเช่น คุณต้องการข้อมูลเกี่ยวกับรสชาติที่ชื่นชอบของเด็กและผู้ใหญ่ ถ้าทั้งสองกลุ่มใหญ่และมีข้อผิดพลาดเล็กน้อย จะทำให้การเปรียบเทียบมีความหมายมากขึ้น
แต่ถ้ากลุ่มหนึ่งมีข้อผิดพลาดมากและอีกกลุ่มมีน้อย การสรุปข้อมูลจากการเปรียบเทียบจะยากขึ้น ข้อผิดพลาดที่มากอาจหมายความว่าความแตกต่างระหว่างกลุ่มอาจไม่สำคัญตามที่ปรากฏ
ความสัมพันธ์ระหว่างการประเมินจุดและข้อผิดพลาดของขอบเขต
ในการสถิติ การประเมินจุดคือค่าที่ใช้เพื่อประเมินพารามิเตอร์ของประชากร โดยคล้ายกับการโยนลูกดอกที่กระดานดอกไม้และหวังว่าจะโดนกลาง แต่ข้อผิดพลาดของขอบเขตบอกเราว่าลูกดอกนั้นใกล้จะโดนกลางมากน้อยเพียงใด
ดังนั้น ข้อผิดพลาดของขอบเขตจึงช่วยให้เราเห็นช่วงที่เราน่าจะพบค่าจริงของการประเมินจุดโดยแสดงถึงการกระจายของค่า
ผลกระทบของข้อผิดพลาดของขอบเขตต่อผลการสำรวจ
เมื่อใช้ข้อมูลจากการสำรวจ ข้อผิดพลาดของขอบเขตมักจะเป็นส่วนสำคัญในการช่วยให้ผู้ชมเข้าใจผลลัพธ์ได้ดียิ่งขึ้น
ข้อผิดพลาดที่เล็กลงแสดงถึงความแม่นยำและความมั่นใจในผลการสำรวจ แต่ข้อผิดพลาดที่มากขึ้นหมายถึงความไม่แน่นอนมากขึ้น
วิธีการลดข้อผิดพลาดของขอบเขต
เมื่อคุณเพิ่มขนาดตัวอย่างหรือลดค่าเบี่ยงเบนมาตรฐาน ข้อผิดพลาดของขอบเขตจะลดลง ทำให้การประเมินใกล้เคียงกับค่าจริงของประชากรมากขึ้น
หากคุณพบว่าข้อผิดพลาดของขอบเขตสูงเกินไปตามระดับความเชื่อมั่นที่ต้องการ คุณควรเพิ่มขนาดตัวอย่างเพื่อให้ข้อมูลที่รวบรวมใกล้เคียงกับค่าจริง
ในโลกของการสำรวจ ข้อผิดพลาดของขอบเขตคือเครื่องมือที่จำเป็นในการให้ความมั่นใจว่าตัวเลขที่ได้ไม่ทำให้เข้าใจผิด
ครั้งหน้าเมื่อคุณเห็นผลการสำรวจที่มีข้อผิดพลาดของขอบเขต ให้ใช้เวลาพิจารณาว่าตัวเลขนั้นหมายถึงอะไรจริงๆ
จำไว้ว่ายิ่งข้อผิดพลาดของคุณเล็กลง คุณก็จะยิ่งมั่นใจในข้อสรุปของคุณมากขึ้น ดังนั้นคุณกำลังรออะไรอยู่? มาคำนวณข้อผิดพลาดของคุณและเริ่มลดความไม่แน่นอนกันเถอะ!
สร้างแบบสำรวจแรกของคุณตอนนี้!
ง่ายเหมือนบีบมะนาว.
- สร้างแบบสำรวจใน 40+ ภาษา
- จำนวนผู้ใช้ไม่จำกัด
- เทมเพลตแบบสำรวจพร้อมใช้กว่า 800 รายการ
- อีกมากมาย...