Taulukon sisältö
Kyselytutkimuksessa virhemarginaalin ymmärtäminen ei ole vain mukavaa, vaan olennaista. Ilman sitä jopa lupaavimmat tulokset voivat olla harhaanjohtavia. Virhemarginaali antaa kontekstia, joka auttaa tekemään tietoon perustuvia päätöksiä kerätyn datan perusteella.
What is the Margin of Error?
Virhemarginaali on tilastollinen käsite, joka kvantifioi epävarmuuden kyselytuloksissasi. Se edustaa aluetta, johon todellisen väestöparametrin odotetaan osuvan, tarjoten tietyn luottamustason ja ottaen huomioon, että kysyt vain otosta väestöstä, ei koko väestöstä.
Pienempi virhemarginaali tarkoittaa, että kyselytuloksesi ovat todennäköisesti lähempänä todellisia väestöarvoja, kun taas suurempi virhemarginaali viittaa suurempaan epävarmuuteen ja laajempaan mahdollisten tulosten alueeseen. Hyväksyttävä virhemarginaali on 4% - 8% 95% luottamustasolla.
Ymmärtäminen tutkimuksessa
Kyselytutkimuksessa virhemarginaali on olennainen, jotta tulosten luotettavuutta voidaan tulkita. LimeSurveyta käytettäessä työskentelet usein väestön otoksen kanssa. Virhemarginaali auttaa ymmärtämään, kuinka lähellä otoksesi tulokset ovat sitä, mitä odottaisit kysyttäessä koko väestöltä.
Virhemarginaalisymbolin selitys ja käyttö
Virhemarginaali usein merkitään symbolilla ± ja jäljessä on prosentti. Esimerkiksi, jos LimeSurvey tuloksesi näyttävät, että 60% vastaajista suosii tiettyä tuotetta virhemarginaalilla ±4%, todellinen väestöarvo on todennäköisesti 56% ja 64% välillä.
Tämä symboli on lyhennystyylinen tapa ilmaista alue, johon todellinen väestöparametri kuuluu. Sitä käytetään laajalti tutkimuksissa, kyselyissä ja missä tahansa tilanteessa, jossa dataa kerätään otoksesta.
Virhemarginaalin laskeminen kolmessa vaiheessa
1. Määritä Z-arvo: Z-arvo vastaa haluttua luottamustasoa, joka kuvaa kuinka kaukana datapiste on keskiarvosta, kokoelman yksikköinä. Esimerkiksi 95% luottamustaso vastaamaan Z-arvoa 1.96 ja 99% Z-arvo 2.58:n.
| Haluttu luottamustaso | Z-arvo |
|---|---|
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
2. Tunnista keskihajonta tai osuus: Keskihajonta mittaa datassasi olevan vaihtelun määrää. Jos käsittelet osuuksia (esim. prosentti vastaajista, joka valitsi tietyn vaihtoehdon), käytät osuutta keskihajonnan sijaan.
3. Laske virhemarginaali tämän kaavan avulla:

𝜎 edustaa keskihajontaa, 𝑛 on otoskoko, ja 𝑍 on Z-arvo. Kaava korostaa kääntäen suhdetta otoskoon ja virhemarginaalin välillä: kun otoskoko kasvaa, virhemarginaali pienenee.
Suurimman otoskoon käyttäminen tuottaa yleensä pienemmän virhemarginaalin, mikä tekee löydöksistäsi luotettavampia. Päinvastoin, pienempi otoskoko johtaa suurempaan virhemarginaaliin, joka heijastaa suurempaa epävarmuutta datassa.
Esimerkiksi, jos kysyt 400 henkilöltä ja löydät, että 50% heistä on tyytyväisiä asiakaskokemukseensa keskihajonnalla 0.5 ja 95% luottamustasolla, virhemarginaali lasketaan seuraavasti:
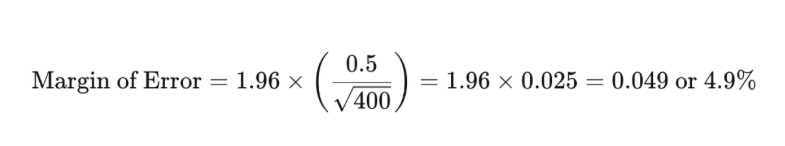
Tämä tarkoittaa, että todellinen prosentti väestöstä, joka on tyytyväinen asiakaskokemukseen, on todennäköisesti välillä 45.1% ja 54.9%.
Virhemarginaalityökalu LimeSurvey-projektiisi
Useat verkossa olevat laskurit voivat auttaa sinua saamaan virhemarginaalin datallesi. Käyttääksesi virhemarginaalilaskuria, sinun on syötettävä haluttu luottamustaso, otoskoko sekä joko keskihajonta tai osuus. Laskuri antaa sitten virhemarginaalin.
Erot virhemarginaalin ja standardivirheen välillä
Virhemarginaali määrittää epävarmuuden kyselytuloksissasi, erityisesti alueen, johon todellisen väestöparametrin odotetaan osuvan otostietosi perusteella. Se on usein esitetty prosenttina ja käytetään antamaan varmuusväli kyselyarviollesi.
Standardivirhe (SE) puolestaan mittaa otosstatistiikan, kuten otoskeskihajonnan, vaihtelua väestön keskiarvosta. Se antaa viitteen siitä, kuinka paljon otosstatistiikka odotetaan vaihtelemaan, jos eri otoksia otettaisiin samasta väestöstä.
Standardivirhe on oleellisempi tilastollisissa testeissä tai eri otosten vertailussa. Virhemarginaali toimii parhaiten keskittyessään yksittäisen kyselyn tuloksen luotettavuuteen, ja standardivirhe on etusijalla tilastojen vertaamisessa otosten välillä.
Parhaat käytännöt virhemarginaalin soveltamiseksi
Kyselytutkimusta tehdessäsi LimeSurveyn avulla seuraa näitä parhaita käytäntöjä virhemarginaalin soveltamiseksi, jotta tutkimuksesi tarkkuus paranee:
- Varmista riittävä otoskoko: Pienemmän virhemarginaalin saavuttamiseksi tutkijoiden tulisi kysyä riittävän suurta otosta, joka edustaa väestöä tarkasti.
- Ota väestön koko huomioon: Vaikka virhemarginaali on pääasiassa riippumaton väestön koosta, on tärkeää ottaa se huomioon käsiteltäessä hyvin pieniä tai hyvin suuria väestöjä.
- Valitse hyväksyttävä luottamustaso: Tyypillisesti tutkijat käyttävät 95% luottamustasoa, joka vastaa Z-arvoa 1.96. Kuitenkin voit valita korkeamman luottamustason, kuten 99%, suuremman varmuuden vuoksi.
- Ole läpinäkyvä: Kun esittelet tutkimustuloksiasi, virhemarginaali auttaa muita ymmärtämään tulostesi mahdollisen vaihtelun ja antaa kontekstia datan tulkitsemiseksi.
- Tarkista säännöllisesti ja säädä: Kun tutkimuksesi etenee tai enemmän dataa tulee saataville, on olennaista tarkistaa virhemarginaalilaskelmasi.
Hyvin laskettu virhemarginaali varmistaa, että kyselytuloksesi ovat luotettavia, heijastelevat laajempaa väestöä ja ovat rehellisiä epävarmuudesta löydöksissäsi – kaikki nämä ovat tärkeitä uskottavuuden ylläpitämiseksi ja tietoon perustuvien päätösten tekemiseksi.
Aloita LimeSurveyllä
LimeSurvey tarjoaa käyttäjäystävällisen ja kattavan kyselytyökalupaketin, joka mahdollistaa erittäin tehokkaiden kyselyjen suunnittelun vaivattomasti. Näiden työkalujen avulla voit luoda hyvin jäsenneltyjä kyselyitä, jotka eivät vain kerää tarvitsemaasi dataa, vaan varmistavat myös, että tuloksesi tulevat optimaalisella virhemarginaalilla.
Tämä tarkoittaa, että kyselysi eivät vain kerää vastauksia – ne tarjoavat luotettavia näkemyksiä, jotka heijastavat kohdeväestösi todellisia tuntemuksia. Olitpa kokenut tutkija tai yliopisto-opiskelija, LimeSurveyn intuitiivinen käyttöliittymä ohjaa sinua joka vaiheessa varmistaen, että kyselydatasi on sekä tarkkaa että toimivaa.



