表格內容
你剛完成一項調查,結果顯示80%的受訪者對你的新產品讚不絕口。雖然你想立即慶祝,但重要的是要記住調查結果底部的小 ± 數字,也就是誤差範圍,因為它可能會成為一個現實檢驗。
在調查研究中,了解誤差範圍不是可有可無,而是至關重要。沒有它,即使是最有希望的結果也可能具有誤導性。誤差範圍提供了上下文,幫助您根據收集到的數據做出明智的決策。
什麼是誤差範圍?
誤差範圍是一項統計數據,量化您的調查結果不確定性。它表示真實人口參數預期落在的範圍,提供特定的信心水平,並考慮到您調查的是樣本而非整個人口。
較小的誤差範圍表示您的調查結果更可能接近真實人口值,而較大的誤差範圍則暗示更大的不確定性和更寬的可能結果範圍。可接受的誤差範圍在95%信心水平時介於4%至8%之間。
理解研究中的誤差範圍
在調查研究中,誤差範圍對於解釋結果的可靠性至關重要。當您使用LimeSurvey收集數據時,您通常在處理人口樣本。誤差範圍幫助您了解樣本結果與若調查整個人口所預期的結果之間的接近程度。
誤差範圍符號的解釋與用法
誤差範圍通常用符號±表示,後面跟隨百分比。假設您的LimeSurvey結果顯示60%的受訪者偏好某特定產品,誤差範圍為±4%。這意味著真實人口值可能介於56%和64%之間。
這個符號是表達真實人口參數所在範圍的一種簡便方式。它在調查投票和任何從樣本中收集數據的情況中廣泛使用。
三步計算誤差範圍
1. 確定Z分數: Z分數對應於所需的信心水平,表示數據點與均值之間的距離,單位為標準差。參考來說,95%信心水平對應的Z分數為1.96,而99%信心水平對應的Z分數為2.58。
| 所需信心水平 | Z分數 |
|---|---|
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
2. 確定標準差或比例: 標準差測量數據的變異量。如果您處理的是比例(例如選擇特定選項的受訪者百分比),則使用比例代替標準差。
3. 使用以下公式計算誤差範圍:

𝜎代表標準差,𝑛是樣本大小,𝑍是Z分數。該公式強調樣本大小與誤差範圍之間的反比關係:樣本大小增加時,誤差範圍減小。
使用較大的樣本大小通常會產生較小的誤差範圍,使您的研究結果更可靠。相反,較小的樣本大小將導致較大的誤差範圍,反映數據中的更大不確定性。
例如,如果您調查400人,發現有50%的人對他們的客戶體驗感到滿意,標準差為0.5,信心水平為95%,則誤差範圍計算如下:
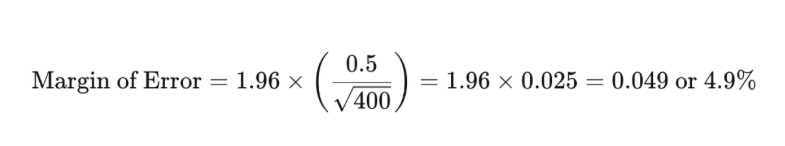
這意味著對於滿意客戶體驗的人口比例很可能介於45.1%和54.9%之間。
LimeSurvey項目的誤差範圍計算器
幾個在線計算器可以幫助您獲取數據的誤差範圍。使用誤差範圍計算器時,您需要輸入所需的信心水平、樣本大小以及標準差或比例。計算器將輸出誤差範圍。
誤差範圍與標準誤的區別
誤差範圍量化了調查結果的不確定性,具體來說是基於您的樣本數據預期真實人口參數的範圍。它通常表達為百分比,用於提供調查估算的信心區間。
另一方面,標準誤(SE)測量樣本統計(如樣本均值)相對於人口均值的變異性或離散性。它指示如果從同一人口中抽取不同樣本,樣本統計將波動的程度。
在進行統計測試或比較不同樣本時,標準誤較為相關。而誤差範圍在聚焦單一調查結果的可靠性時效果更佳,而標準誤則在比較樣本間的統計數據時更受青睞。
應用誤差範圍的最佳實踐
在使用LimeSurvey進行研究時,遵循這些最佳實踐應用誤差範圍可提高研究的準確性:
- 確保樣本大小足夠: 為了實現較低的誤差範圍,研究人員應調查足夠大的樣本,以準確代表整個人口。
- 考慮人口大小: 雖然誤差範圍大多與人口大小無關,但在處理非常小或非常大的人口時,考慮它仍然很重要。
- 選擇可接受的信心水平: 研究人員通常使用95%信心水平,對應的Z分數為1.96。然而,您可能選擇較高的信心水平,如99%,以獲得更大確定性。
- 保持透明: 在呈現研究結果時,誤差範圍幫助他人理解結果的潛在變異性,並為解釋數據提供上下文。
- 定期回顧和調整: 隨著研究進展或新數據的出現,定期檢查您的誤差範圍計算是必要的。
良好的誤差範圍計算可確保您的調查結果值得信賴,能真實反映更廣泛的人口,並誠實地表達結果中的不確定性,這些都是維持可信度和做出明智決策所必需的。
開始使用LimeSurvey
LimeSurvey提供了一套用戶友好且全面的調查工具,使您能輕鬆設計高效的調查。利用這些工具,您可以創建結構良好的調查,不僅能捕獲所需數據,還能確保結果帶有最佳的誤差範圍。
這意味著您的調查不僅僅是收集回應——它們還將提供您可以信任的見解,反映目標人口的真實情感。無論您是經驗豐富的研究人員還是大學生,LimeSurvey的直觀界面將在每一步引導您,確保您的調查數據既準確又可操作。



