表格内容
你刚完成了一项调查,结果显示80%的受访者对你的新产品赞不绝口。虽然你想立即庆祝,但要记得调查结果底部的小±数字,也就是误差范围,因为它可能会成为一个现实检查。
在调查研究中,了解误差范围不仅是有益的,而是至关重要的。没有它,即使是最有前景的结果也可能具有误导性。误差范围提供了上下文,帮助您根据收集的数据做出知情决策。
什么是误差范围?
误差范围是量化调查结果不确定性的统计数据。它表示真实总体参数预期落入的范围,提供一定的置信水平,并考虑到您仅对总体的一部分进行调查。
较小的误差范围表明您的调查结果更可能接近真实的总体值,而较大的误差范围则暗示更大的不确定性和更广泛的可能结果。可接受的误差范围在95%置信水平下为4%到8%之间。
研究中的误差范围理解
在调查研究中,误差范围对于解释结果的可靠性至关重要。当您使用LimeSurvey收集数据时,您通常是在处理总体的一个样本。误差范围帮助您理解样本结果与整个总体调查预期的接近程度。
误差范围符号的解释和使用
误差范围通常用符号±表示,并跟随一个百分比。假设您的LimeSurvey结果显示60%的受访者偏好某产品,误差范围为±4%。这意味着真实的总体值可能在56%到64%之间。
该符号是表达真实总体参数所在范围的简写形式,广泛用于调查、民意调查以及任何从样本中收集数据的场景。
三步计算误差范围
1. 确定Z值:Z值对应于所需的置信水平,表示数据点距离均值的标准差单位。参考而言,95%置信水平的Z值为1.96,而99%置信水平的Z值为2.58。
| 所需置信水平 | Z值 |
|---|---|
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
2. 确定标准差或比例:标准差衡量数据的变异程度。如果您处理的是比例(例如选择特定选项的受访者百分比),则使用比例代替标准差。
3. 使用此公式计算误差范围:

𝜎表示标准差,𝑛为样本大小,𝑍为Z值。该公式强调样本大小与误差范围之间的反比关系:样本大小增加,误差范围减小。
使用更大的样本大小通常会产生更小的误差范围,使您的发现更可靠。相反,较小的样本大小将导致更大的误差范围,反映出数据的不确定性。
例如,若您对400人进行调查,发现50%的人对客户体验满意,标准差为0.5且置信水平为95%,则误差范围的计算如下:
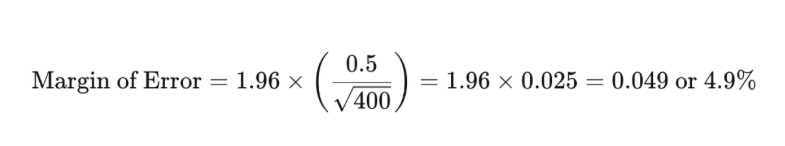
这意味着真实满意的总体百分比可能在45.1%到54.9%之间。
LimeSurvey项目的误差范围计算器
有多个在线计算器可以帮助您获取数据的误差范围。使用误差范围计算器时,您需输入所需的置信水平、样本大小,以及标准差或比例。计算器将输出误差范围。
误差范围与标准误差的区别
误差范围量化调查结果的不确定性,特指基于样本数据真实总体参数预期落入的范围。它通常以百分比表示,并用于为调查估计提供置信区间。
而标准误差(SE)度量样本统计量(如样本均值)与总体均值的变异性或离散性。它显示如果从同一总体抽取不同样本,样本统计量预计会有多大的波动。
进行统计测试或比较不同样本时,标准误差更为相关。而误差范围在关注单一调查结果的可靠性时效果最佳,标准误差在跨样本比较统计时更受青睐。
应用误差范围的最佳实践
在使用LimeSurvey进行研究时,遵循这些最佳实践可提高您研究的准确性:
- 确保样本大小充足:为实现较低的误差范围,研究人员应调查一个足够大的样本,以准确反映总体。
- 考虑总体大小:虽然误差范围在很大程度上独立于总体大小,但在处理非常小或非常大的总体时,考虑总体大小是重要的。
- 选择可接受的置信水平:通常,研究人员使用95%置信水平,对应的Z值为1.96。不过,您也可以选择更高的置信水平,如99%,以获得更大的确定性。
- 保持透明:在呈现研究结果时,误差范围帮助他人理解您结果的潜在变异性,并提供解释数据的上下文。
- 定期审查和调整:随着研究的进行或更多数据的可用,审查您的误差范围计算是必要的。
良好计算的误差范围确保您的调查结果可信、反映更广泛的人群,并坦诚关于您发现的不确定性,这些都是维持可信度和做出知情决策的关键。
开始使用LimeSurvey
LimeSurvey提供了一套用户友好且全面的调查工具,使您轻松设计高效的调查。通过这些工具,您可以创建结构良好的调查,不仅收集所需的数据,还确保您的结果具有最佳的误差范围。
这意味着您的调查不仅收集回应,还能提供您可以信任的洞察,反映目标人群的真实情感。无论您是经验丰富的研究人员还是大学生,LimeSurvey直观的界面都会在每一步指导您,确保您的调查数据既准确又可操作。



