テーブルコンテンツ
あなたは調査を終え、その結果が出ました—80%の回答者があなたの新製品を絶賛しています。すぐに祝いたい気持ちもありますが、調査結果の下にある±数値、いわゆる誤差範囲を忘れないことが重要です。これが現実を確認する手助けになるかもしれません。
調査研究の世界において、誤差範囲を理解することは不可欠です。これがないと、最も有望な結果さえも誤解を招く可能性があります。誤差範囲はコンテキストを提供し、収集したデータに基づいて情報に基づいた意思決定を行う手助けをします。
誤差範囲とは何か?
誤差範囲は調査結果の不確実性を定量化する統計です。これは、真の母集団パラメータが予想される範囲を表し、一定の信頼水準を提供し、全体ではなく母集団のサンプルを調査しているという事実を考慮します。
小さい誤差範囲は、調査結果が真の母集団値に近い可能性が高いことを示し、大きい誤差範囲は不確実性が高く、可能性のある結果の範囲が広いことを示します。許容される誤差範囲は95%の信頼水準で4%から8%の間です。
研究における誤差範囲の理解
調査研究において、誤差範囲は結果の信頼性を解釈するために重要です。LimeSurveyを使ってデータを収集する際には、母集団のサンプルを扱っていることが多いです。誤差範囲は、サンプル結果が全体の母集団を調査した場合に予想される値にどれだけ近いかを理解するのに役立ちます。
誤差範囲の記号の説明と使用法
誤差範囲は通常、記号±で表され、その後にパーセンテージが続きます。例えば、LimeSurveyの結果が60%の回答者が特定の商品を好み、誤差範囲が±4%である場合、真の母集団値は56%から64%の間にある可能性があります。
この記号は、真の母集団パラメータが存在する範囲を表現する短縮形です。調査やデータ収集のシナリオで広く使用されます。
誤差範囲を計算する3つのステップ
1. Zスコアを決定する: Zスコアは望ましい信頼水準に対応し、データポイントが平均から標準偏差の単位でどれだけ離れているかを表します。参考までに、95%の信頼水準はZスコア1.96に関連し、99%は2.58に相当します。
| 望ましい信頼水準 | Zスコア |
|---|---|
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
2. 標準偏差または割合を特定する: 標準偏差はデータの変動量を測定します。割合(特定の選択肢を選んだ回答者の割合)の場合、標準偏差の代わりに割合を使用します。
3. この公式を使って誤差範囲を計算する:

𝜎は標準偏差、𝑛はサンプルサイズ、𝑍はZスコアです。この公式は、サンプルサイズと誤差範囲の逆関係を強調します:サンプルサイズが増加すると、誤差範囲は減少します。
大きなサンプルサイズを使用すれば、通常は小さい誤差範囲が得られ、結果がより信頼性のあるものとなります。一方、小さいサンプルサイズは大きな誤差範囲になり、データに対する不確実性が高くなります。
例えば、400人を調査して、そのうち50%が顧客体験に満足しており、標準偏差が0.5、95%の信頼水準の場合、誤差範囲は次のように計算されます:
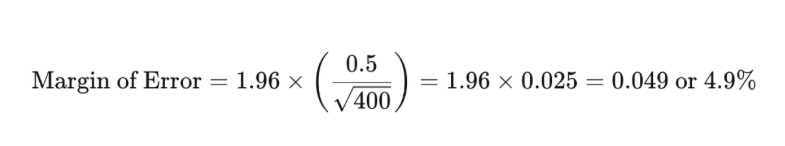
これにより、顧客体験に満足している真の割合は45.1%から54.9%の間にあると予想されます。
LimeSurveyプロジェクトのための誤差範囲計算機
データの誤差範囲を取得するためのいくつかのオンライン計算機があります。誤差範囲計算機を使用するには、望ましい信頼水準、サンプルサイズ、および標準偏差または割合を入力する必要があります。計算機は誤差範囲を出力します。
誤差範囲と標準誤差の違い
誤差範囲は、調査結果の不確実性を定量化し、サンプルデータに基づいて真の母集団パラメータが予想される範囲を示します。通常、パーセンテージとして表現され、調査推定値の信頼区間を提供するために使用されます。
一方、標準誤差(SE)は、サンプル統計(例えば、サンプル平均)が母集団平均からどれだけ変動するかを測定します。これは、同じ母集団から異なるサンプルが引かれた場合にサンプル統計がどれほど変動するかの指標となります。
標準誤差は統計テストや異なるサンプルの比較を行う際により関連性があります。誤差範囲は、単一の調査結果の信頼性に焦点を当てる際に最も効果的であり、標準誤差はサンプル間での統計の比較に使用されます。
誤差範囲の適用に関するベストプラクティス
LimeSurveyを使用して研究を行う際は、誤差範囲の適用に関する以下のベストプラクティスを守ることで、研究の精度を向上させることができます:
- 十分なサンプルサイズを確保する: 低い誤差範囲を達成するためには、研究者は母集団を忠実に代表する十分に大きなサンプルを調査する必要があります。
- 母集団サイズを考慮する: 誤差範囲は主に母集団サイズに依存しませんが、非常に小さいまたは非常に大きい母集団を扱う際には考慮が重要です。
- 許容される信頼水準を選択する: 研究者は通常、Zスコア1.96に相当する95%の信頼水準を使用しますが、より高い信頼水準(99%など)を選択することも可能です。
- 透明性を保つ: 研究成果を提示する際、誤差範囲は結果の変動可能性を理解するのに役立ち、データ解釈の文脈を提供します。
- 定期的に見直し、調整する: 研究が進むにつれて、あるいは新たなデータが利用可能になるにつれて、誤差範囲計算を見直すことが重要です。
適切に計算された誤差範囲は、調査結果が信頼でき、より広い母集団を反映し、発見における不確実性について誠実であることを保証します。これは、信頼性を維持し、情報に基づいた意思決定を行う上で重要です。
LimeSurveyを始める
LimeSurveyは、非常に効果的な調査を簡単に設計できるユーザーフレンドリーで包括的な調査ツールを提供します。これらのツールを使用すれば、必要なデータをキャッチし、最適な誤差範囲で結果を確保できるしっかりした調査を作成できます。
つまり、あなたの調査は単に回答を集めるだけでなく、ターゲット母集団の実際の感情を反映する信頼できる洞察を提供します。経験豊富な研究者であれ、大学生であれ、LimeSurveyの直感的なインターフェースが手助けし、調査データが正確かつ実用的であることを保証します。



