Хүснэгт агуулга

Та судалгаагаа дуусгасан бөгөөд үр дүн нь гарчээ—хариултлагчдын 80% нь таны шинэ бүтээгдэхүүнийг үнэлж байна. Тэгэхээр даруй баярлаж эхлэхийг хүсээд байвал, судалгааны үр дүнгийн доод талын ± тоог, буюу алдааны хязгаарын талаар санах нь чухал—учир нь энэ нь бодит байдлыг шалгахын тулд гарах боломжтой.

Судалгааны судалгаанд алдааны хязгаар (margin of error)-ын ойлголт нь зүгээр л хэрэгтэй зүйл биш, харин ч зайлшгүй шаардлагатай. Энэ нь судалгааны үр дүнг үнэн зөв ойлгоход тусалдаг.

Алдааны Хязгаар гэж юу вэ?

Алдааны хязгаар нь судалгааны үр дүнгийн үл итгэлтэй байдлыг тооцоолох статистик мэдээ юм. Энэ нь бодит хүн амын параметр ямар хүрээнд байхыг илэрхийлж, тодорхой итгэлцлийн түвшинг тэмдэглэдэг.

Алдааны хязгаар бага байх нь таны судалгааны үр дүн нь бодит хүн амын утгадаа ойртох магадлал ихтэй, харин их алдааны хязгаар нь ихэнхдээ илүү үл итгэлтэй байхыг илэрхийлнэ. Зөвшөөрөгдсөн алдааны хязгаар 4% - 8% өгөөмөр итгэлцлийн түвшинд байна.

Судалгаанд Алдааны Хязгаарын Ойлголт

Судалгааны дүнг тайлбарлахад алдааны хязгаар чухал юм. LimeSurvey ашиглан өгөгдөл цуглуулж байхдаа хүн амын төдийлөн ихэнхийг биш, ширхэг жишиг авч ажиллаж байх хэрэгтэй. Алдааны хязгаар нь жишиг үр дүн нь хүн амын нийт хүн амд очвол ямар байхад ойр байхыг ойлгоход тусална.

Алдааны Хязгаарын Символын Тайлбар ба Ашиглалт

Алдааны хязгаар ихэвчлэн ± симболоор дүрслэгддэг бөгөөд хувьцаар дагалддаг. Жишээлбэл, хэрвээ танай LimeSurvey-ийн үр дүн 60% хариулт гаргасныг ±4% алдааны хязгаартай гэж үзвэл, бодит хүн амын утга 56% - 64% хооронд байх магадлалтай.

Энэ симбол нь бодит хүн амын параметр аль хүрээнд байхыг илэрхийлсэн товчилсон хэлбэр юм. Судалгааны санал асуулгад, жишигд отогт авсан өгөгдөлд өргөнөөр хэрэглэгддэг.

Алдааны Хязгаарыг 3 Алхамд Тооцоолох

1. Z-скорыг тодорхойлох: Z-скор нь хүссэн итгэлцлийн түвшинд хамаарна. 95% итгэлцлийн түвшин 1.96 Z-скортой, 99% итгэлцлийн түвшин 2.58 Z-скортой.

Итгэлцлийн түвшинZ-скор
80% 1.28
85% 1.44
90% 1.65
95% 1.96
99% 2.58

2. Стандарт хазайлт эсвэл хувь хэмжээг тодорхойлох: Стандарт хазайлт нь өгөгдлийн ялгааг хэмждэг. Хэрвээ хувь хэмжээг авч үзвэл стандарт хазайлтын оронд хувь хэмжээг ашиглана.

3. Энэ формулыг ашиглан алдааны хязгаарыг тооцоолох:

Алдааны хязгаар тооцоолох формула

𝜎 стандарт хазайлт, 𝑛 жишиг хэмжээ, 𝑍 Z-скор. Формула жишиг хэмжээ болон алдааны хязгаарын хоорондын шилжих харилцааг онцолж байна: жишиг хэмжээ ихсэхэд алдааны хязгаар багасна.

Том жишиг хэмжээ ихэвчлэн бага алдааны хязгаар гаргах ба таны судалгааг илүү найдвартай болгодог. Харин жижиг жишиг хэмжээ нь илүү их алдааны хязгаар үүсгэх бөгөөд өгөгдөлд ихээр үл итгэлтэй байдлыг илтгэнэ.

Жишээлбэл, хэрвээ та 400 хүнийг судалж, тэдний 50% нь хэрэглэгчийн туршлагаас сэтгэл хангалуун байгаа бөгөөд стандарт хазайлт 0.5, 95% итгэлцлийн түвшинтэй бол алдааны хязгаарыг тактикийн дараах байдлаар тооцоолох болно:

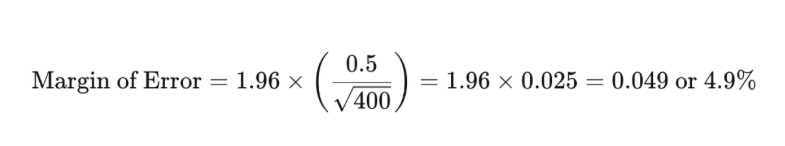
алдааны хязгаарын формула

Энэ нь бодит хувь хэмжээ нь хэрэглэгчийн туршлагаас сэтгэл хангалуун байгаа нь 45.1% - 54.9% хооронд байж магадгүйг илтгэнэ.

LimeSurvey Төслийн Алдааны Хязгаар Тооцоолох Хэрэгсэл

Таны өгөгдлийн алдааны хязгаарыг олоход туслах олон онлайн тооцоолох хэрэгсэл байдаг. Алдааны хязгаарын тооцоолох хэрэгслийг ашиглахын тулд хүссэн итгэлцлийн түвшин, жишиг хэмжээ, стандарт хазайлт эсвэл хувь хэмжээг оруулна. Тооцоолох хэрэгсэл нь алдааны хязгаарыг гаргана.

Алдааны Хязгаар болон Стандарт Алдаа хоорондын Ялгаанууд

Алдааны хязгаар нь судалгааны үр дүнгийн үл итгэлтэй байдлыг тооцоолдог бөгөөд жишиг өгөгдлөөр дамжуулан бодит параметр аль хүрээнд байхыг тооцоолно. Энэ нь ихэвчлэн хувьцаар илэрхийлэгддэг бөгөөд судалгааны үнэлгээг тойрон итгэлцлийн интервал бий болгоход хэрэглэгддэг.

Мөн стандарт алдаа (SE) нь жишиг статистикийн хувь хэмжээ хүний тоогоор ялгааг хэмждэг, жишиг дундаас хамгийн их зөрүүг тодорхойлдог. Энэ нь өөр өөр жишгээс гарсан хүлээгдэж буй статистикийн жишиг дунд нь хэр их хэлбэлзэхийг илтгэнэ.

Стандарт алдаа нь статистикийн тест хийхэд илүү чухал байж, жишиг дүнг харьцуулахад чухал. Алдааны хязгаар нь ганц судалгааны дүнг найдвартай харуулахад илүү тохиромжтой, стандарт алдаа нь жишгийг харьцуулахдаа чухал.

Алдааны Хязгаар хэрэглэх шилдэг практик

LimeSurvey ашиглан судалгаа хийхдээ алдааны хязгарыг ашиглах шилдэг практикуудаар судалгааныхаа нарийн байдлыг сайжруулах боломжтой:

  • Зохих жишиг хэмжээг хангах: Бага алдааны хязгаар авахын тулд судлаачид хүн амын жишгийг сайн төлөөлүүлэхуйц хангалттай том жишиг хэмжээг судлах хэрэгтэй.
  • Хүн амын хэмжээг харгалзах: Алдааны хязгаар ихэнхдээ хүн амын хэмжээнээс бие даан боловч маш жижиг, эсвэл их хүн амтай бол үүнийг харгалзаж үзэх нь чухал юм.
  • Зөвшөөрөгдөх итгэлцлийн түвшинг сонгох: Судлаачид ихэвчлэн 95% итгэлцлийн түвшин хэрэглэдэг, энэ нь 1.96 Z-скортой. Гэвч их илүү итгэлтэй байх үүднээс 99% итгэлцлийн түвшнийг сонгож болно.
  • Ил тод байх: Судалгааны дүнг танилцуулахдаа алдааны хязгаар нь бусдад таны дүнгийн магадлалыг ойлгоход тусална.
  • Тогтмол шалгаж, шинэчлэх: Судалгаа явуулж байхдаа алдааны хязгаарын тооцооллыг тогтмол шалгаж, шинэчлэх шаардлагатай.

Сайтар тооцоолсон алдааны хязгаар нь таны судалгааны үр дүнг найдвартай, өргөн хүрээний хүн амын төлөөллийг харуулахад, мөн таны олж авсан үр дүнд илүү үнэнч байх хэрэгтэй - эдгээр нь итгэдэг байдал болон мэдээлэлтэй шийдвэр гаргахад чухал ач холбогдолтой.

LimeSurvey-тай Ашиглахыг Эхлэх

LimeSurvey нь судалгааг үр дүнтэй байдлаар зохион байгуулахад зориулагдсан хялбар бөгөөд иж бүрэн хэрэгслүүдийг санал болгодог. Эдгээр хэрэгслүүдээр та нарийн бүтэцтэй судалгаа хийж, шаардлагатай өгөгдлийг бүгдийг нь цуглуулах боломжтой бөгөөд алдааны хязгаар нь хамгийн оптималь байх болно.

Энэ нь таны судалгаанууд зөвхөн хариулт авахгүй, бас таны зорилтот хүн амын бодит сэтгэлгээний тусхангуй мэдээллийг өгнө гэсэн үг. Та судалгааны эрхмийн хүн эсвэл их сургуулийн студент бай, LimeSurvey-ийн ойлгомжтой интерфейс нь таны судалгааны өгөгдлийг үнэн зөв, ашиглаж болохуйц болгоход дэмжлэг үзүүлэх болно.