คู่มือฉบับสมบูรณ์ในการเข้าใจขอบเขตความผิดพลาด

LimeSurvey เสนอโซลูชันที่ใช้งานง่ายสำหรับการออกแบบแบบสอบถาม ทำให้ผู้คนสามารถสร้างแบบสอบถามที่มีข้อมูลเชิงลึกและผลลัพธ์ที่มีความหมายได้อย่างง่ายดาย มาสำรวจเคล็ดลับที่จะช่วยให้คุณออกแบบการสำรวจที่เหมาะสมกันเถอะ 1. วางแผน วิเคราะห์ และรายงาน ก่อนเริ่มการสำรวจให้พิจารณาโครงสร้างรายงานและประเภทการวิเคราะห์ที่ควรทำ การมองเห็นผลลัพธ์สุดท้ายจะช่วยให้คุณระบุคำถามที่ต้องการและตัวเลือกการตอบกลับที่เกี่ยวข้อง พร้อมทั้งตรวจสอบสิ่งที่ขาดหายไปในแบบสอบถาม 2. ใช้คำถามและมาตราส่วนการตอบกลับที่ได้รับการตรวจสอบแล้ว การตรวจสอบว่าคำถามของคุณตรงตามเกณฑ์พื้นฐานในการรวบรวมข้อมูลที่ไม่มีอคติเป็นวิธีประหยัดเวลาในการรวบรวมข้อมูลที่เชื่อถือได้ ควรใช้ภาษาที่เข้าใจง่าย คำถามที่ไม่มีความคลุมเครือ และหลีกเลี่ยงคำถามที่ยาวและซับซ้อน หากคุณไม่แน่ใจว่าจะเริ่มต้นอย่างไร ลองดูมาตราส่วนการประเมินเหล่านี้: มาตราส่วนลิเคิร์ต: ใช้ได้ทั่วไปในการวัดทัศนคติ ความชอบ และการรับรู้ในงานวิจัยสังคมศาสตร์ มาตราส่วนความแตกต่างเชิงอรรถ: ให้ข้อมูลเชิงลึกเกี่ยวกับความหมายร่วมของสิ่งต่างๆ งาน และแนวคิด 3. ใช้คำถามหลายรูปแบบ รวมคำถามประเภทต่างๆ เช่น หลายตัวเลือก เปิดกว้าง และการจัดอันดับ เพื่อรวบรวมข้อมูลที่หลากหลายและได้รับคำตอบที่ถูกต้อง 4. พิจารณาวิธีการสำรวจที่ผ่านการพิสูจน์แล้ว การใช้วิธีการสำรวจที่เป็นที่ยอมรับจะช่วยเพิ่มความน่าเชื่อถือ จงพิจารณาสองวิธีนี้: การวิเคราะห์ร่วม: เทคนิคทางสถิติในการวิจัยตลาดเพื่อหามูลค่าที่ผู้คนนิยมในลักษณะต่างๆ มิเตอร์ความรู้สึกด้านราคา Van Westendorp: วิธีการที่ช่วยกำหนดความชอบด้านราคาในกลุ่มผู้บริโภค 5. ผสานอุปกรณ์การสำรวจ อุปกรณ์การสำรวจประกอบไปด้วยเครื่องมือและเทคนิคที่ออกแบบมาเพื่อรวบรวมข้อมูลจากผู้เข้าร่วมอย่างเป็นระบบ Net Promoter Score (NPS): เครื่องมือวัดความภักดีของลูกค้าและคาดการณ์การเติบโตของธุรกิจ Customer Satisfaction Score (CSAT): เครื่องมือที่ตรงไปตรงมาสำหรับวัดความพึงพอใจของลูกค้าในทันที Gallup Q12: ชุดคำถาม 12 ข้อที่เน้นความมุ่งมั่นและความพึงพอใจของพนักงาน Utrecht Work Engagement Scale (UWES): มาตราสำหรับวัดความมุ่งมั่นของพนักงาน Students' Evaluation of Educational Quality (SEEQ): การประเมินคุณภาพการศึกษาในมุมมองของนักเรียน Hospital Consumer Assessment of Healthcare Providers and Systems (HCAHPS): มาตรฐานสำหรับวัดมุมมองของผู้ป่วยเกี่ยวกับการดูแลในโรงพยาบาล Maslach Burnout Inventory (MBI): วิธีการสำหรับวัดระดับความเหนื่อยหน่ายของพนักงาน 6. ใช้รูปแบบที่ใช้งานง่าย การมีรูปแบบการสำรวจที่ใช้งานง่ายจะช่วยให้แบบฟอร์มดูดี ใช้งานง่าย และเข้าถึงได้จากอุปกรณ์และขนาดหน้าจอที่ต่างกัน 7. คิดถึงกลุ่มเป้าหมายและขนาดของตัวอย่าง พิจารณาประชากรศาสตร์ของกลุ่มเป้าหมาย รวมถึง อายุ เพศ ระดับการศึกษา และภูมิหลังทางวัฒนธรรม เพื่อให้คุณสามารถปรับเนื้อหาและภาษาของแบบสอบถามให้เหมาะสม 8. คำนึงถึงมาตรฐานการทดลองออนไลน์ แนวทางเหล่านี้ช่วยรับประกันคุณภาพและความถูกต้องของการศึกษาวิจัย ความจริงจัง: ผู้วิจัยควรรักษาความเป็นมืออาชีพ และให้คำแนะนำที่ชัดเจน การปรับให้เป็นส่วนตัว: ทำให้ประสบการณ์การสำรวจเป็นส่วนตัวเพื่อให้ผู้เข้าร่วมรู้สึกมีค่า รางวัลและแรงจูงใจ: พิจารณาให้รางวัลหรือแรงจูงใจแก่ผู้เข้าร่วม 9. ลดอคติ ดำเนินการเพื่อลดอคติในการตอบกลับซึ่งอาจทำให้ผลสำรวจไม่ถูกต้อง 10. ทดลองก่อน ทำการทดสอบเบื้องต้นก่อนเผยแพร่การสำรวจให้กับกลุ่มกว้าง เพื่อตรวจหา ปัญหาที่เป็นไปได้ LimeSurvey ช่วยให้คุณสร้างแบบสอบถามที่ไม่มีอคติและครอบคลุม ซึ่งตรงตามความต้องการในการศึกษา เริ่มต้นการสำรวจของคุณได้แล้ววันนี้ และรวบรวมข้อมูลเชิงลึกเพื่อสนับสนุนการวิจัย

การสร้างแบบสำรวจออนไลน์อาจดูเหมือนเป็นงานง่าย – เพียงแค่คิดคำถาม กรอกข้อมูลแล้วส่งไปใช่ไหม? แต่การสร้างแบบสำรวจที่ประสบความสำเร็จเพื่อดึงดูดผู้ตอบ สนับสนุนพวกเขา และให้ข้อมูลและข้อคิดเห็นที่มีค่า ต้องใช้เวลา ความคิด และแผนงานมากมาย นี่คือเจ็ดคำแนะนำที่ควรพิจารณาขณะจัดทำแบบสำรวจครั้งถัดไปของคุณ: 1. วางแผนแบบสำรวจของคุณอย่างรอบคอบ เมื่อคิดถึงแบบสำรวจ มักมุ่งเน้นที่เนื้อหาของคำถามและประเภทการตอบกลับที่หวังจะได้รับ แต่การคิดล่วงหน้าเกี่ยวกับวิธีวิเคราะห์ข้อมูลสำรวจจะช่วยในการปรับแต่งคำถามและตัวเลือกการตอบกลับ รวมถึงทำให้แบบสำรวจของคุณมีประสิทธิภาพและประสบความสำเร็จมากขึ้น ดีที่รู้: ด้วย LimeSurvey คุณสามารถส่งออกคำตอบแบบสำรวจในรูปแบบข้อมูลที่หลากหลาย รวมถึง Excel และซอฟต์แวร์สำรวจเฉพาะอย่าง R หรือ SPSS Statistics 2. เคารพความเป็นส่วนตัวและการปกป้องข้อมูล การทำให้แน่ใจว่าแบบสำรวจของคุณสอดคล้องกับกฎหมายการปกป้องข้อมูลเช่น GDPR และการรับประกันความเป็นส่วนตัวจะช่วยลดความกังวลของผู้ตอบเกี่ยวกับการใช้คำตอบของพวกเขา ดีที่รู้: คุณลักษณะความเป็นส่วนตัวที่เกี่ยวข้อง เช่น การตอบแบบไม่ระบุชื่อหรือการเข้ารหัสจะมีให้ใน LimeSurvey Cloud และสามารถปรับแต่งได้ตามต้องการ 3. รู้จักกลุ่มเป้าหมายของคุณ ไม่ว่าคุณจะเสนอแบบสำรวจความพึงพอใจของพนักงานหรือความพึงพอใจของลูกค้า รู้จักกลุ่มเป้าหมายที่เฉพาะเจาะจงเป็นสิ่งสำคัญ หากคุณต้องการความคิดเห็นจากจำนวนคนที่จำกัด งานนี้มักจะง่าย แต่หากคุณมีกลุ่มผู้ตอบที่ใหญ่ ข้อปฏิบัติที่ดีที่สุดคือการสุ่มตัวอย่างจากกลุ่มที่เกี่ยวข้องที่คุณต้องการความคิดเห็นจาก ดีที่รู้: LimeSurvey มีการรวมแผนการที่ทำให้การรวมผู้ตอบจากผู้ให้บริการแผนได้ง่ายขึ้น เริ่มต้นกับ LimeSurvey 4. ปรับแต่งแบบสอบถามให้เหมาะสมกับผู้ตอบ สิ่งที่ดีเกี่ยวกับแบบสอบถามออนไลน์คือคุณสามารถสร้างประสบการณ์แบบสอบถามที่แตกต่างกันสำหรับผู้ตอบแต่ละคน โดยใช้ข้อมูลที่คุณรวบรวมไว้แล้ว 5. ตรวจสอบคำตอบแบบสำรวจ แม้จะดูเหมือนว่าวิธีที่ดีที่สุดคือการรอให้แบบสำรวจปิดก่อนดูการตอบกลับ การตรวจสอบข้อมูลขณะสำรวจดำเนินการอยู่จะช่วยให้คุณทราบหากมีปัญหาใด ๆ ดีที่รู้: LimeSurvey ให้ผู้ใช้เข้าถึงคำตอบแบบสำรวจได้โดยตรง เพื่อให้คุณตรวจสอบข้อมูลได้โดยไม่ต้องส่งออก 6. ใช้มาตรการเพื่อให้ได้คุณภาพข้อมูลสูง ก่อนเริ่มการวิเคราะห์ข้อมูล ต้องตรวจสอบคุณภาพของข้อมูล เพื่อช่วยตัดสินส่วนของการสำรวจที่ไม่สมบูรณ์หรือซ้ำซ้อน 7. ทำงานเพื่อให้ได้รับอัตราการตอบกลับสูง ถึงแม้คุณอาจไม่ได้รับอัตราการเข้าร่วม 100% แต่มีวิธีในการกระตุ้นให้ผู้คนเข้าร่วม โดยเฉพาะอย่างยิ่งการให้เวลามากพอในการตอบ ดีที่รู้: LimeSurvey มีตัวเลือกในการบันทึกและกลับมาทำแบบสอบถามทั้งแบบปิดและแบบเปิด การคำนึงถึงเจ็ดข้อแนะนำนี้ขณะวางแผนแบบสำรวจของคุณจะช่วยให้คุณมั่นใจในตารางเวลา ปรับปรุงแบบสอบถาม และตั้งเป้าหมายสู่ความสำเร็จ ด้วย LimeSurvey คุณสามารถสร้างและปรับแต่งแบบสำรวจตามความต้องการของคุณ สำหรับข้อมูลเพิ่มเติมเกี่ยวกับการเริ่มต้นหรือการใช้เครื่องมือต่าง ๆ สามารถดูได้ที่ ศูนย์ช่วยเหลือ. เริ่มต้นกับ LimeSurvey

ในโลกของงานวิจัยสำรวจ การเข้าใจขอบเขตความผิดพลาด (Margin of Error) ไม่ใช่แค่สิ่งที่ดี แต่จำเป็นอย่างยิ่ง หากไม่มีอาจทำให้ผลการสำรวจที่ดูมีแนวโน้มสูงกลายเป็นข้อมูลที่เข้าใจผิด ขอบเขตความผิดพลาดช่วยให้คุณตัดสินใจได้อย่างมีข้อมูลจากข้อมูลที่เก็บมา ขอบเขตความผิดพลาดคืออะไร? ขอบเขตความผิดพลาดเป็นสถิติที่บ่งบอกความไม่แน่นอนในผลการสำรวจ มันแสดงถึงช่วงที่คาดว่าพารามิเตอร์ประชากรที่แท้จริงจะอยู่ โดยให้ระดับความเชื่อมั่น และคำนึงถึงว่าคุณสำรวจจากกลุ่มตัวอย่างแทนที่จะเป็นประชากรทั้งหมด ขอบเขตความผิดพลาดที่เล็กกว่าบ่งบอกว่าผลการสำรวจของคุณมีแนวโน้มที่จะใกล้เคียงกับค่าจริงของประชากร ขณะที่ขอบเขตที่ใหญ่กว่าชี้ให้เห็นถึงความไม่แน่นอนที่มากขึ้น โดยค่าที่ยอมรับได้จะอยู่ระหว่าง 4% ถึง 8% ในระดับความเชื่อมั่น 95% ความเข้าใจขอบเขตความผิดพลาดในการวิจัย ในงานวิจัยสำรวจ ขอบเขตความผิดพลาดเป็นสิ่งจำเป็นในการตีความความเชื่อถือได้ของผลลัพธ์ เมื่อคุณเก็บข้อมูลโดยใช้ LimeSurvey คุณมักจะทำงานกับกลุ่มตัวอย่างจากประชากร ขอบเขตความผิดพลาดช่วยให้คุณเข้าใจว่าผลลัพธ์จากกลุ่มตัวอย่างของคุณใกล้เคียงกับสิ่งที่คุณคาดหวังหากคุณสำรวจประชากรทั้งหมดอย่างไร คำอธิบายและการใช้งานสัญลักษณ์ขอบเขตความผิดพลาด ขอบเขตความผิดพลาดมักแสดงด้วยสัญลักษณ์ ± ตามด้วยเปอร์เซ็นต์ ยกตัวอย่างเช่น ผลการสำรวจจาก LimeSurvey แสดงว่า 60% ของผู้ตอบแบบสอบถามชอบผลิตภัณฑ์บางอย่าง โดยมีขอบเขตความผิดพลาด ±4% หมายความว่าค่าจริงของประชากรน่าจะอยู่ระหว่าง 56% ถึง 64% สัญลักษณ์นี้เป็นวิธีการแสดงช่วงที่พารามิเตอร์ประชากรที่แท้จริงอยู่ โดยทั่วไปแล้วจะใช้ในงานวิจัย การสำรวจ และกรณีที่เก็บข้อมูลจากกลุ่มตัวอย่าง คำนวณขอบเขตความผิดพลาดใน 3 ขั้นตอน 1. กำหนดค่า Z-score: ค่า Z-score จะเกี่ยวข้องกับระดับความเชื่อมั่นที่ต้องการ โดยแสดงถึงระยะห่างของข้อมูลจากค่าเฉลี่ยในหน่วยส่วนเบี่ยงเบนมาตรฐาน สำหรับอ้างอิง ระดับความเชื่อมั่น 95% สัมพันธ์กับ Z-score ที่ 1.96 ขณะที่ระดับ 99% สัมพันธ์กับ Z-score ที่ 2.58 ระดับความเชื่อมั่นที่ต้องการZ-score 80% 1.28 85% 1.44 90% 1.65 95% 1.96 99% 2.58 2. ระบุส่วนเบี่ยงเบนมาตรฐานหรือสัดส่วน: ส่วนเบี่ยงเบนมาตรฐานวัดปริมาณความแปรปรวนในข้อมูลของคุณ หากคุณจัดการกับสัดส่วน (เช่น เปอร์เซ็นต์ของผู้ตอบที่เลือกตัวเลือกเฉพาะ) คุณจะใช้สัดส่วนแทนส่วนเบี่ยงเบนมาตรฐาน 3. คำนวณขอบเขตความผิดพลาดโดยใช้สูตรนี้: 𝜎 แทนส่วนเบี่ยงเบนมาตรฐาน, 𝑛 คือขนาดกลุ่มตัวอย่าง และ 𝑍 คือค่า Z-score สูตรนี้แสดงให้เห็นถึงความสัมพันธ์ที่ตรงกันข้ามระหว่างขนาดกลุ่มตัวอย่างและขอบเขตความผิดพลาด: เมื่อขนาดกลุ่มตัวอย่างเพิ่มขึ้น ขอบเขตความผิดพลาดจะลดลง การใช้ขนาดกลุ่มตัวอย่างที่ใหญ่ขึ้นจะทำให้ขอบเขตความผิดพลาดเล็กลง ทำให้ผลลัพธ์ของคุณเชื่อถือได้มากขึ้น ในทางกลับกัน ขนาดกลุ่มตัวอย่างที่เล็กจะส่งผลให้มีขอบเขตความผิดพลาดที่ใหญ่ขึ้น ซึ่งสะท้อนถึงความไม่แน่นอนที่มากขึ้นในข้อมูล เช่น หากคุณสำรวจคน 400 คนและพบว่า 50% ของพวกเขาพอใจกับประสบการณ์ของลูกค้า โดยมีส่วนเบี่ยงเบนมาตรฐาน 0.5 และระดับความเชื่อมั่น 95% การคำนวณขอบเขตความผิดพลาดจะทำได้ดังนี้: 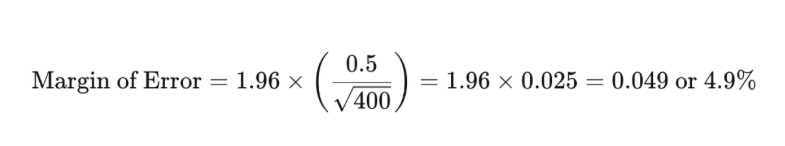ซึ่งหมายความว่าร้อยละที่แท้จริงของประชากรที่พอใจกับประสบการณ์ของลูกค้าน่าจะอยู่ระหว่าง 45.1% ถึง 54.9% เครื่องคำนวณขอบเขตความผิดพลาดสำหรับโครงการ LimeSurvey ของคุณ มีเครื่องคำนวณออนไลน์หลายตัวที่ช่วยให้คุณคำนวณขอบเขตความผิดพลาดได้ง่ายเพื่อข้อมูลของคุณ โดยป้อนระดับความเชื่อมั่นที่ต้องการ ขนาดกลุ่มตัวอย่าง และเลือกส่วนเบี่ยงเบนมาตรฐานหรือสัดส่วน เครื่องคำนวณจะคำนวณขอบเขตความผิดพลาดให้คุณ ความแตกต่างระหว่างขอบเขตความผิดพลาดและข้อผิดพลาดมาตรฐาน ขอบเขตความผิดพลาดวัดความไม่แน่นอนในผลการสำรวจของคุณ โดยเฉพาะช่วงที่พารามิเตอร์ประชากรที่แท้จริงคาดว่าจะอยู่ตามข้อมูลตัวอย่าง ส่วนข้อผิดพลาดมาตรฐาน (SE) วัดการแปรปรวนหรือการกระจายของสถิติจากกลุ่มตัวอย่าง เช่น ค่าเฉลี่ยจากกลุ่มตัวอย่างที่แตกต่างกับค่าเฉลี่ยในประชากร ข้อผิดพลาดมาตรฐานมีความสำคัญมากเมื่อทำการทดสอบเชิงสถิติหรือเปรียบเทียบกลุ่มตัวอย่างต่างๆ ขอบเขตความผิดพลาดเหมาะสมที่สุดเมื่อมุ่งเน้นที่ความเชื่อถือได้ของผลการสำรวจเดียว ขณะที่ข้อผิดพลาดมาตรฐานจะpreferableเมื่อเปรียบเทียบสถิติระหว่างกลุ่มตัวอย่าง แนวทางที่ดีที่สุดสำหรับการใช้ขอบเขตความผิดพลาด เมื่อดำเนินการวิจัยโดยใช้ LimeSurvey ให้ปฏิบัติตามแนวทางที่ดีที่สุดเหล่านี้เพื่อการใช้ขอบเขตความผิดพลาดให้ส่งผลดีต่อความแม่นยำของการศึกษา: 确保样本量充足：为了获得较低的误差范围，研究人员应调查足够大的样本，准确代表总体。 考虑总体数量：虽然误差范围大部分不受总体数量影响，但在处理非常小或非常大的人群时，仍需考虑这一点。 选择可接受的信心水平：通常，研究人员使用95％的置信水平，这对应于Z-score为1.96。但是，您可能会选择更高的置信水平，如99％以获得更大的确定性。 保持透明：在呈现研究发现时，误差范围帮助他人理解您结果中潜在的可变性，并为解读数据提供背景。 定期审查和调整：随着您的研究进展或获取更多数据，确保定期检查您对误差范围的计算。 การคำนวณขอบเขตความผิดพลาดที่ดีช่วยให้ผลการสำรวจของคุณเชื่อถือได้ สะท้อนถึงประชากรในวงกว้าง และจริงใจกับความไม่แน่นอนในผลการวิจัยของคุณ ซึ่งทั้งหมดนี้มีความสำคัญต่อการรักษาเครดิตและการตัดสินใจอย่างมีข้อมูล เริ่มต้นกับ LimeSurvey LimeSurvey มีชุดเครื่องมือสำรวจที่ใช้งานง่ายและครอบคลุม ช่วยให้คุณออกแบบการสำรวจที่มีประสิทธิภาพได้อย่างง่ายดาย ด้วยเครื่องมือเหล่านี้ คุณสามารถสร้างการสำรวจที่มีโครงสร้างดี ซึ่งไม่เพียงแต่เก็บข้อมูลที่คุณต้องการ แต่ยังมั่นใจได้ว่าผลลัพธ์ของคุณมีขอบเขตความผิดพลาดที่เหมาะสม ซึ่งหมายความว่าการสำรวจของคุณจะไม่เพียงแต่เก็บการตอบสนอง แต่จะให้ข้อมูลเชิงลึกที่คุณเชื่อถือได้ สะท้อนความรู้สึกที่แท้จริงของประชากรเป้าหมายของคุณ ไม่ว่าคุณจะเป็นนักวิจัยที่มีประสบการณ์หรือเป็นนักเรียนมหาวิทยาลัย อินเทอร์เฟซที่เข้าใจง่ายของ LimeSurvey จะช่วยให้คุณทุกขั้นตอน ทำให้ข้อมูลการสำรวจของคุณถูกต้องและใช้งานได้ สร้างการสำรวจตอนนี้