Tabelleninhalt
Du hesch grad e Umfrag abgschlosse und dini Resultat si do—80% vo de Befragte schwärme vo dim neue Produkt. Obschon du sofort feire wotsch, isch es wichtig, sich an die kleine ± Zahl z erinnere, au bekannt als d'Fehlergrenze, am Ende vo dinene Resultate—denn die könnte dir e Realitätstest geba.
Im Bereich der Umfrageforschung ist das Verständnis des Fehlerintervalls nicht nur wünschenswert, sondern essenziell. Ohne dieses kann selbst das vielversprechendste Ergebnis irreführend sein. Das Fehlerintervall liefert den Kontext, der hilft, informierte Entscheidungen basierend auf den gesammelten Daten zu treffen.
Was ist das Fehlerintervall?
Das Fehlerintervall ist eine Statistik, die die Unsicherheit Ihrer Umfrageergebnisse quantifiziert. Es stellt den Bereich dar, in dem der wahre Bevölkerungsparameter voraussichtlich liegt, bietet ein gewisses Vertrauensniveau und berücksichtigt, dass Sie eine Stichprobe der Bevölkerung anstelle der gesamten Bevölkerung befragen.
Ein kleineres Fehlerintervall deutet darauf hin, dass Ihre Umfrageergebnisse näher an den tatsächlichen Bevölkerungswerten liegen, während ein größeres Fehlerintervall auf eine größere Unsicherheit und ein breiteres Spektrum möglicher Ergebnisse hinweist. Ein akzeptables Fehlerintervall liegt zwischen 4% und 8% bei einem Vertrauensniveau von 95%.
Das Fehlerintervall in der Forschung verstehen
In der Umfrageforschung ist das Fehlerintervall entscheidend für die Interpretation der Zuverlässigkeit Ihrer Ergebnisse. Wenn Sie Daten mit LimeSurvey sammeln, arbeiten Sie oft mit einer Stichprobe der Bevölkerung. Das Fehlerintervall hilft Ihnen zu verstehen, wie nah Ihre Stichproben Ergebnisse dem entsprechen, was Sie erwarten würden, wenn Sie die gesamte Bevölkerung befragen würden.
Erläuterung und Verwendung des Fehlersymbols
Das Fehlerintervall wird typischerweise durch das Symbol ± dargestellt, gefolgt von einem Prozentsatz. Wenn Ihre LimeSurvey-Ergebnisse zeigen, dass 60% der Befragten ein bestimmtes Produkt bevorzugen, mit einem Fehlerintervall von ±4%, bedeutet das, dass der wahre Bevölkerungswert wahrscheinlich zwischen 56% und 64% liegt.
Dieses Symbol ist eine abgekürzte Art, den Bereich auszudrücken, in dem der wahre Bevölkerungsparameter liegt. Es wird häufig in der Forschung, Umfragen und in jedem Szenario verwendet, in dem Daten aus einer Stichprobe gesammelt werden.
Berechnung des Fehlerintervalls in 3 Schritten
1. Bestimmen Sie den Z-Wert: Der Z-Wert entspricht dem gewünschten Vertrauensniveau und gibt an, wie weit ein Datenpunkt vom Mittelwert in Standardabweichungseinheiten entfernt ist. Zum Vergleich: Ein Vertrauensniveau von 95% hat einen Z-Wert von 1.96, während ein Vertrauensniveau von 99% einem Z-Wert von 2.58 entspricht.
| Gewünschtes Vertrauensniveau | Z-Wert |
|---|---|
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
2. Bestimmen Sie die Standardabweichung oder Proportion: Die Standardabweichung misst die Variation in Ihren Daten. Wenn Sie mit Proportionen arbeiten (z.B. der Prozentsatz der Befragten, die eine bestimmte Option gewählt haben), verwenden Sie die Proportion anstelle der Standardabweichung.
3. Berechnen Sie das Fehlerintervall mit dieser Formel:

𝜎 steht für die Standardabweichung, 𝑛 ist die Stichprobengröße, und 𝑍 ist der Z-Wert. Die Formel verdeutlicht die umgekehrte Beziehung zwischen Stichprobengröße und Fehlerintervall: Wenn die Stichprobengröße zunimmt, verringert sich das Fehlerintervall.
Eine größere Stichprobengröße führt in der Regel zu einem kleineren Fehlerintervall, wodurch Ihre Ergebnisse zuverlässiger werden. Im Gegensatz dazu ergibt eine kleinere Stichprobe ein größeres Fehlerintervall, was eine größere Unsicherheit in den Daten widerspiegelt.
Zum Beispiel, wenn Sie 400 Personen befragen und feststellen, dass 50% von ihnen mit ihrer Kundenerfahrung zufrieden sind, mit einer Standardabweichung von 0.5 und einem Vertrauensniveau von 95%, würde das Fehlerintervall wie folgt berechnet:
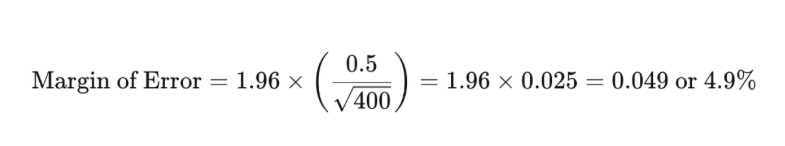
Das bedeutet, dass der wahre Prozentsatz der Bevölkerung, der mit der Kundenerfahrung zufrieden ist, wahrscheinlich zwischen 45.1% und 54.9% liegt.
Fehlerintervall-Rechner für Ihr LimeSurvey-Projekt
Es gibt mehrere Online-Rechner, die Ihnen helfen können, das Fehlerintervall für Ihre Daten zu ermitteln. Um einen Fehlerintervall-Rechner zu verwenden, müssen Sie das gewünschte Vertrauensniveau, die Stichprobengröße und entweder die Standardabweichung oder die Proportion eingeben. Der Rechner gibt Ihnen dann das Fehlerintervall aus.
Unterschiede zwischen Fehlerintervall und Standardfehler
Das Fehlerintervall quantifiziert die Unsicherheit in Ihren Umfrageergebnissen, insbesondere den Bereich, in dem der wahre Bevölkerungsparameter basierend auf Ihren Stichprobendaten erwartet wird. Es wird häufig als Prozentsatz ausgedrückt und dient zur Bereitstellung eines Vertrauensintervalls um eine Schätzung der Umfrage.
Der Standardfehler (SE) hingegen misst die Variabilität oder Streuung einer Stichprobenstatistik, wie z.B. den Stichprobenmittelwert vom Populationsmittelwert. Er gibt einen Hinweis darauf, wie sehr die Stichprobenstatistik schwanken kann, wenn unterschiedliche Stichproben aus derselben Population gezogen werden.
Der Standardfehler ist relevanter bei statistischen Tests oder beim Vergleich verschiedener Stichproben. Das Fehlerintervall ist am besten geeignet, wenn man sich auf die Zuverlässigkeit eines einzelnen Umfrageergebnisses konzentriert, während der Standardfehler bevorzugt wird, wenn Statistiken über Stichproben hinweg verglichen werden.
Beste Praktiken für die Anwendung des Fehlerintervalls
Bei der Durchführung von Forschung mit LimeSurvey sollten Sie diese besten Praktiken zur Anwendung des Fehlerintervalls befolgen, um die Genauigkeit Ihrer Studie zu verbessern:
- Ausreichende Stichprobengröße sicherstellen: Um ein niedriges Fehlerintervall zu erreichen, sollten Forscher eine ausreichend große Stichprobe befragen, die die Bevölkerung genau repräsentiert.
- Bevölkerungsgröße berücksichtigen: Während das Fehlerintervall größtenteils unabhängig von der Bevölkerungsgröße ist, ist es wichtig, dies bei sehr kleinen oder sehr großen Bevölkerungen zu berücksichtigen.
- Ein akzeptables Vertrauensniveau wählen: Typischerweise verwenden Forscher ein Vertrauensniveau von 95%, das einem Z-Wert von 1.96 entspricht. Sie könnten jedoch ein höheres Vertrauensniveau wie 99% für größere Sicherheit wählen.
- Transparenz: Bei der Präsentation Ihrer Forschungsergebnisse hilft das Fehlerintervall anderen, die potenzielle Variabilität Ihrer Ergebnisse zu verstehen und kontextuelle Informationen zur Interpretation der Daten bereitzustellen.
- Regelmäßig überprüfen und anpassen: Wenn Ihre Forschung fortschreitet oder neue Daten verfügbar werden, ist es wichtig, Ihre Berechnungen zum Fehlerintervall zu überprüfen.
Ein gut berechnetes Fehlerintervall stellt sicher, dass Ihre Umfrageergebnisse vertrauenswürdig sind, die breitere Bevölkerung widerspiegeln und ehrlich über jegliche Unsicherheit in Ihren Ergebnissen informieren – allesamt entscheidend für die Aufrechterhaltung von Glaubwürdigkeit und informierten Entscheidungen.
Starten Sie mit LimeSurvey
LimeSurvey bietet eine Reihe benutzerfreundlicher und umfassender Umfragetools, die es Ihnen ermöglichen, hoch effektive Umfragen mühelos zu gestalten. Mit diesen Tools können Sie gut strukturierte Umfragen erstellen, die nicht nur die Daten erfassen, die Sie benötigen, sondern sicherstellen, dass Ihre Ergebnisse mit einem optimalen Fehlerintervall einhergehen.
Das bedeutet, dass Ihre Umfragen nicht nur Antworten sammeln – sie liefern vertrauenswürdige Erkenntnisse, die die wahren Ansichten Ihrer Zielpopulation widerspiegeln. Egal, ob Sie ein erfahrener Forscher oder ein Universitätsstudent sind, die intuitive Benutzeroberfläche von LimeSurvey führt Sie Schritt für Schritt durch den Prozess und stellt sicher, dass Ihre Umfragedaten sowohl genau als auch umsetzbar sind.



